Chapitre 4
Agrandissement et réduction
Chapitre 4 : Agrandissement et réduction
A) Agrandissement et réduction d'une figure
Définition : Faire un agrandissement d’une figure c’est multiplier toutes les longueurs par un même nombre $k$ supérieur à 1 en conservant la forme de la figure.
Vocabulaire : $k$ est appelé le rapport d’agrandissement.
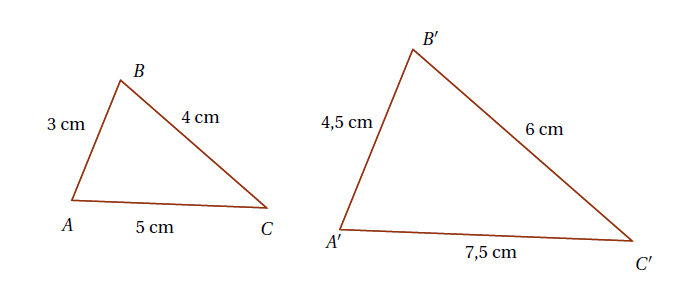
Exemple : Sur la figure ci-dessous, le triangle $A’B’C’$ est un agrandissement du triangle $ABC$. Les longueurs ont été multipliées par 1,5. En effet :
\[3\times 1,5=4,5~~~~4\times 1,5=6~~~~5\times 1,5=7,5\]
Les dimensions de la figure obtenue lors d’un agrandissement sont proportionnelles à celles de la figure initiale.
\[\dfrac{4,5}{3}=\dfrac{6}{4}=\dfrac{7,5}{5}=\textcolor{red}{1,5}\]
Définition : Faire une réduction d’une figure c’est multiplier toutes les longueurs par un même nombre $k$ compris entre 0 et 1 en conservant la forme de la figure.
Vocabulaire : $k$ est appelé le rapport de réduction.
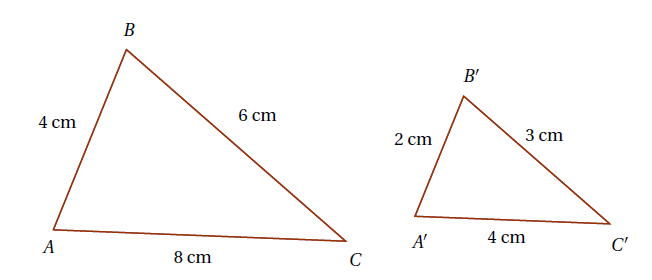
Exemple : Sur la figure ci-dessous, le triangle $A’B’C’$ est une réduction du triangle $ABC$. Les longueurs ont été multipliées par 0,5. En effet :
\[4\times 0,5=2~~~~6\times 0,5=3~~~~8\times 0,5=4\]
Les dimensions de la figure obtenue lors d’une réduction sont proportionnelles à celles de la figure initiale.
\[\dfrac{2}{4}=\dfrac{3}{6}=\dfrac{4}{8}=\textcolor{red}{0,5}\]
B) Conservation des angles et du parallélisme
Conséquence : Lors de l’agrandissement ou de la réduction d’une figure :
- les mesures des angles sont conservées (donc la perpendicularité en particulier) ;
- le parallélisme est conservé.
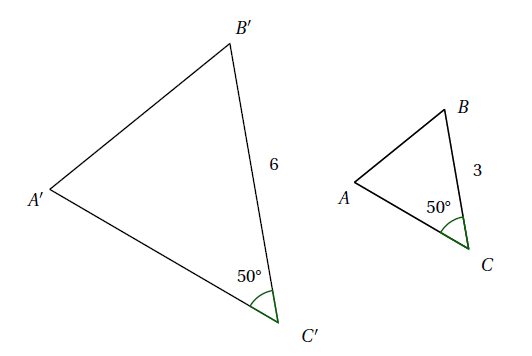
Exemple : Le triangle $A’B’C’$ est un agrandissement du triangle $ABC$ dans le rapport 2. Donc :
\[ C’B’=2\times CB\]\[\widehat{ACB}=\widehat{A’B’C’}\]
C) Effet sur les aires
Propriété : Si les longueurs d’une figure sont multipliées par un nombre $k$ (positif), alors l’aire est multipliée par $k^{2}$.
Exemple : Sur la figure ci-dessous, le rectangle $A’B’C’D’$ est un agrandissement du rectangle $ABCD$ de coefficient 3.
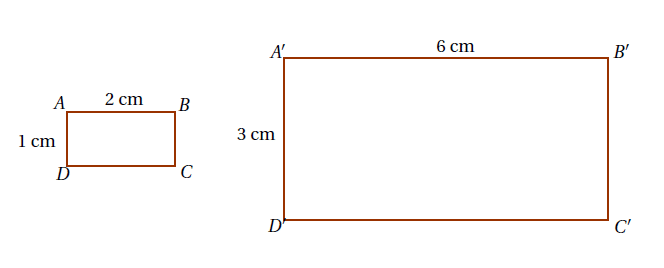
Or :
$A_{ABCD}=1~\text{cm}\times 2~\text{cm}=2~\text{cm}^{2}$
$A_{A’B’C’D’}=3~\text{cm}\times 6~\text{cm}=18~\text{cm}^{2}$
L’aire a été multipliée par $3^{2}=9$.
Exemple : La surface d’un champ est de 12 hectares. On multiplie ses dimensions par 2,5. Quelle sera sa nouvelle surface?
\begin{eqnarray*}
A_{nouvelle~surface}&=&2,5^{2}\times A_{surface~de~départ}\\
&=&2,5^{2}\times 12~\text{hectares}\\
&=&75~\text{hectares}
\end{eqnarray*}
D) Effet sur les volumes
Propriété : Si les longueurs d’une figure sont multipliées par un nombre $k$ (positif), alors le volume est multiplié par $k^{3}$.
Exemple : Sur la figure ci-dessous, le 2ème pavé droit est un agrandissement du 1er pavé droit de coefficient 2.
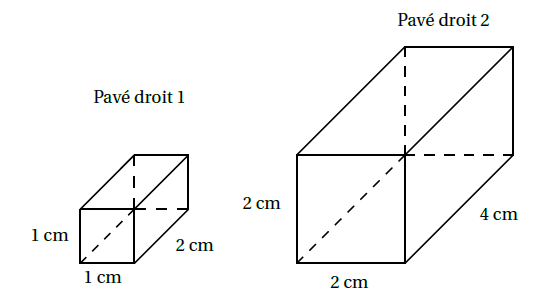
Or :
$V_{pavé~droit~1}=1~\text{cm}\times 1~\text{cm}\times 2~\text{cm}=2~\text{cm}^{3}$
$V_{pavé~droit~2}=2~\text{cm}\times 2~\text{cm}\times 4~\text{cm}=16~\text{cm}^{3}$
Le volume a été multiplié par $2^{3}=8$.