Section d'excellence
Somme d'entiers consécutifs

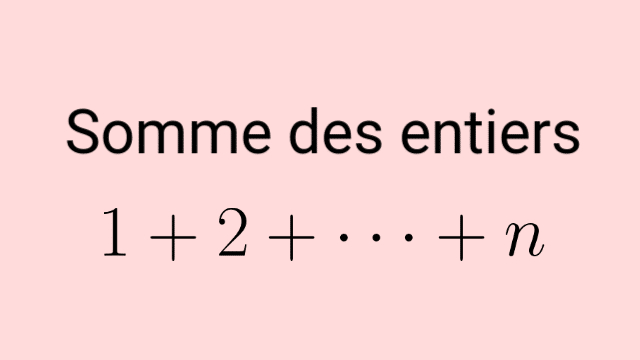
Sujet : Que peut-on dire de la somme de plusieurs entiers consécutifs ?
Définition : Des entiers naturels consécutifs sont des entiers naturels qui se suivent immédiatement. Exemple : 234 ; 235 et 236 sont des entiers naturels consécutifs Nous nous sommes intéressés à la propriété suivante : Propriété : la somme de trois entiers consécutifs est un multiple de trois. Voici quelques exemple :- Les nombres 17,18 et 19 sont trois entiers naturels consécutifs.
- Les nombres 5,6 et 7 sont trois entiers naturels consécutifs.
 Nous avons ensuite essayé de voir si la propriété restait vraie avec quatre nombres entiers naturels consécutifs? Obtenons-nous un multiple de 4 ?
exemple : 13 + 14 + 15 + 16 = 58
58/ 4 = 14,5
14,5 n’étant pas dans la table de 4, donc 58 n’est pas un multiple de 4. Il est démontré que la somme de 4 entier naturels consécutifs n’est pas un multiple de 4.
En revanche, pour la somme de 5 entiers naturels consécutifs, cela fonctionne.
En effet : 1 + 2 + 3 + 4 + 5 = 15 et 15 est bien un multiple de 5.
Démonstration :
on appelle n l’entier du milieu :
n – 2 + n – 1 + n + n + 1 + n + 2 = 5n
5n est bien l’écriture d’un multiple de 5.
Nous avons ensuite essayé de voir si la propriété restait vraie avec quatre nombres entiers naturels consécutifs? Obtenons-nous un multiple de 4 ?
exemple : 13 + 14 + 15 + 16 = 58
58/ 4 = 14,5
14,5 n’étant pas dans la table de 4, donc 58 n’est pas un multiple de 4. Il est démontré que la somme de 4 entier naturels consécutifs n’est pas un multiple de 4.
En revanche, pour la somme de 5 entiers naturels consécutifs, cela fonctionne.
En effet : 1 + 2 + 3 + 4 + 5 = 15 et 15 est bien un multiple de 5.
Démonstration :
on appelle n l’entier du milieu :
n – 2 + n – 1 + n + n + 1 + n + 2 = 5n
5n est bien l’écriture d’un multiple de 5.

 Finalement, nous avons voulu montrer que la somme des 999 premiers entiers consécutifs est égale à 499 500.
1 + 2 + 3 + … + 999 = 499 500 ?
Avec un regroupement astucieux des termes de cette somme, nous y sommes parvenus (sans utiliser de calculatrice !) :
1 + 2 + 3 + … +999
= (1+ 999) + (2 + 998) + (3 + 997) +…+ (499 + 501) + 500
= 499 x 1000 + 500
= 499 500
Deux fichiers Scratch à télécharger :
Finalement, nous avons voulu montrer que la somme des 999 premiers entiers consécutifs est égale à 499 500.
1 + 2 + 3 + … + 999 = 499 500 ?
Avec un regroupement astucieux des termes de cette somme, nous y sommes parvenus (sans utiliser de calculatrice !) :
1 + 2 + 3 + … +999
= (1+ 999) + (2 + 998) + (3 + 997) +…+ (499 + 501) + 500
= 499 x 1000 + 500
= 499 500
Deux fichiers Scratch à télécharger :