Actualités

Visite de la maison Poincaré

Laisser un commentaire /

Section d'excellence

La maison Poincaré

Cours de mathématiques de 4ème
La semaine dernière, les élèves de la section excellence ont visité la maison Poincaré au coeur de Paris. Durant la première heure, un intervenant du musée leur a proposé une visite de certaines salles du musée : Dans la salle Partager , ils ont exploré une numération différente grâce à une carte spatio-temporelle interactive. Dans la salle Connecter , la carte du “métro mathématique” leur a permis de visualiser les innombrables liens entre les différents domaines des mathématiques. C’est à cette occasion qu’ils ont découvert le célèbre théorème des quatre couleurs. Enfin, ils ont plongé dans l’univers fascinant de la topologie en manipulant le Rulpidon, emblème du musée.     Lors de la deuxième partie de la visite, un doctorant leur a expliqué comment les mathématiques sont mises au service de la rédaction de sa thèse en santé publique.  

Visite de la maison Poincaré Lire la suite »

Suite de Farey et cercles de Ford

Laisser un commentaire /

Section d'excellence

Suite de Farey et cercles de Ford

Cours de mathématiques de 4ème

A) Introduction

Extrait du document les fractions de Monsieur Farey, Robert FERACHOGLOU, Lycée Le Castel à Dijon :

Le géologue anglais John Farey suggéra en 1816 de ranger dans l’ordre croissant les fractions irréductibles, comprises entre 0 et 1, et dont le dénominateur ne dépasse pas une valeur donnée.
Par exemple, celles dont le dénominateur est inférieur ou égal à 3 se rangent ainsi :

\[\dfrac{0}{1},\dfrac{1}{3},\dfrac{1}{2},\dfrac{2}{3},\dfrac{1}{1}\]

Farey remarqua qu’une telle suite possédait de jolies propriétés. Cependant Farey, qui n’était qu’un mathématicien moyen (et même un géologue quelconque, puisqu’il est aujourd’hui presque entièrement oublié en tant que tel), ne donna aucune preuve des résultats publiés. C’est Louis Augustin Cauchy qui démontra les propriétés en question ; ce dernier, bon prince, a conservé le nom de Farey attaché à ces suites de fractions.

Ce document propose de mettre en évidence quelques propriétés des suites de Farey et des cercles de Ford.

B) Définitions et premières conjectures

Définition : La suite de Farey de rang $n$, noté $F_{n}$ , est la suite finie formée par les fractions irréductibles de dénominateur inférieur ou égal à $n$ comprises entre 0 et 1, rangées dans l’ordre croissant.

Exemples :

  • $F_{1}=\left(\dfrac{0}{1},\dfrac{1}{1}\right)$
  • $F_{2}=\left(\dfrac{0}{1},\dfrac{1}{2},\dfrac{1}{1}\right)$
  • $F_{3}=\left(\dfrac{0}{1},\dfrac{1}{3},\dfrac{1}{2},\dfrac{2}{3},\dfrac{1}{1}\right)$

Définition : Soient deux fractions consécutifs $\dfrac{a}{b}$ et $\dfrac{c}{d}$ d’une suite de Farey.

On appelle fraction médiane des fractions $\dfrac{a}{b}$ et $\dfrac{c}{d}$ la fraction $\dfrac{p}{q}$ telle que :

\[\dfrac{p}{q}=\dfrac{a+c}{b+d}\]

Dans un premier, les élèves de la section ont déterminé $F_{4}$, $F_{5}$ et $F_{6}$ :

  • $F_{4}=\left(\dfrac{0}{1},\dfrac{1}{4},\dfrac{1}{3},\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},\dfrac{1}{1}\right)$
  • $F_{5}=\left(\dfrac{0}{1},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{1}{2},\dfrac{3}{5},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5},\dfrac{1}{1}\right)$
  • $F_{6}=\left(\dfrac{0}{1},\dfrac{1}{6},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{1}{2},\dfrac{3}{5},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5},\dfrac{5}{6},\dfrac{1}{1}\right)$
Voici quelques conjectures émises par les élèves :
    1. La fraction $\dfrac{1}{2}$ occupe la position médiane dans $F_{n}$.
    2. En choisissant deux fractions consécutives de $F_{n}$ (notées $\dfrac{a}{b}<\dfrac{c}{d}$) et en calculant $bc-ad$, on obtient toujours $1$ : \[bc-ad=1\]
    3. Si $\dfrac{a}{b}$, $\dfrac{e}{f}$ et $\dfrac{c}{d}$ sont, dans cet ordre, trois fractions successives d’une même suite de Farey, alors (addition des cancres)  :\[\dfrac{e}{f}=\dfrac{a+c}{b+d}\]
    4. $F_n$ est la réunion de $F_{n-1}$ et de l’ensemble des fractions médianes de $F_{n-1}$ de dénominateur égal à $n$.

Remarques :

  1. La première conjecture n’a pas été démontrée en classe.
  2. La deuxième conjecture n’a également pas été démontrée en classe mais vérifiée dans certains cas :
    Dans $F_{5}$, on choisit $\dfrac{a}{b}=\dfrac{2}{5}$ et $\dfrac{c}{d}=\dfrac{1}{2}$. On obtient alors :
    \[bc-ad=5\times 1-2\times 2=5-4=1\]
  3. La troisième conjecture peut-être démontrée en classe avec les très bons élèves :
    Démonstration : Soient 3 termes consécutifs d’une suite de Farey : $\dfrac{a}{b}<\dfrac{p}{q}<\dfrac{c}{d}$.
    On a donc :
    \[
    \left \{
    \begin{array}{c @{=} c}
    pb-aq = 1 \\
    cq-pd = 1
    \end{array}
    \right.
    \]On multiplie la première équation par $c$ et la deuxième par $a$ :
    \[
    \left \{
    \begin{array}{c @{=} c}
    pb-aq =1~~~~\times c \\
    cq-pd =1~~~~\times a
    \end{array}
    \right.
    \]On multiplie la première équation par $d$ et la deuxième par $b$ :
    \[
    \left \{
    \begin{array}{c @{=} c}
    pb-aq = 1~~~~\times d \\
    cq-pd = 1~~~~\times b
    \end{array}
    \right.
    \]On obtient alors :
    \[
    \left \{
    \begin{array}{c @{=} c}
    pbc-aqc = c \\
    cqa-pda = a
    \end{array}
    \right.
    \]

    \[
    \left \{
    \begin{array}{c @{=} c}
    pbd-aqd = d\\
    cqb-pdb = b
    \end{array}
    \right.
    \]Par somme :
    \[pbc-pad=a+c\]

    \[
    cqb-adq=b+d
    \]On en déduit en factorisant les membres de gauche :
    \[
    \left \{
    \begin{array}{c @{=} c}
    p(bc-ad) = a+c\\
    q(bc-ad) = b+d
    \end{array}
    \right.
    \]Par quotient :
    \[\dfrac{p(bc-ad)}{q(bc-ad)}=\dfrac{a+c}{b+d}\]Ainsi, en simplifiant par $(bc-ad)$ :
    \[\dfrac{p}{q}=\dfrac{a+c}{b+d}\]

  4. Les fractions de $F_7$ sont ainsi obtenues en ajoutant aux fractions de $F_6$ l’ensemble des fractions médianes de $F_6$ de dénominateur égal à 6. Par ailleurs, les fractions médianes de $F_6$ sont les premières à apparaître entre deux fractions de $F_7$. Ainsi :
    $F_{7}=\left(\dfrac{0}{1},\dfrac{1}{7},\dfrac{1}{6},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{3}{7},\dfrac{1}{2},\dfrac{4}{7},\dfrac{3}{5},\dfrac{2}{3},\dfrac{5}{7},\dfrac{3}{4},\dfrac{4}{5},\dfrac{5}{6},\dfrac{6}{7},\dfrac{1}{1}\right)$

C) Lien avec les cercles de Ford

Le mathématicien américain Lester Randolph Ford (1886-1975), spécialiste en théorie des nombres, se pencha à titre ludique sur les fractions de Farey. Il en donna en 1917 une propriété géométrique étonnante, que nous allons développer ci-dessous.

Définition : Soient $a$ et $b$ deux entiers non nuls. On représente sur l’axe des abscisses et au dessus de chaque fraction $\dfrac{a}{b}$
le cercle de rayon $\dfrac{1}{2b^{2}}$ , appelé cercle de Ford de $\dfrac{a}{b}$.

Exemples : Les cercles de Ford associés à $F_{1}$, $F_{2}$, $F_{3} et $F_{6}$.

Les élèves ont conjecturé que les cercles de Ford associés à deux termes consécutifs d’une même suite de Farey sont tangents entre eux.

Démonstration : Voici la preuve pour les cercles de Ford associés aux fractions $\dfrac{1}{3}$ et $\dfrac{1}{2}$ :


On a :

  • $0_{1}A=\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3}{6}-\dfrac{2}{6}=\dfrac{1}{6}$
  • $0_{2}A=\dfrac{1}{2\times 2^{2}}-\dfrac{1}{2\times 3^{2}}=\dfrac{1}{8}-\dfrac{1}{18}=\dfrac{9}{72}-\dfrac{4}{72}=\dfrac{5}{72}$

Le triangle $O_{1}O_{2}A$ est rectangle en $A$.
D’après le théorème de Pythagore :
\begin{eqnarray*}
O_{1}O_{2}^{2}&=&0_{1}A^{2}+0_{2}A^{2}\\
O_{1}O_{2}^{2}&=&\left(\dfrac{1}{6}\right)^{2}+\left(\dfrac{5}{72}\right)^{2}\\
O_{1}O_{2}^{2}&=&\dfrac{1}{36}+\dfrac{25}{5~184}\\
O_{1}O_{2}^{2}&=&\dfrac{144}{5~184}+\dfrac{25}{5~184}\\
O_{1}O_{2}^{2}&=&\dfrac{169}{5~184}\\
O_{1}O_{2}&=&\sqrt{\dfrac{169}{5~184}}\\
O_{1}O_{2}&=&\dfrac{13}{72}
\end{eqnarray*}
Or : $O_{1}I+IO_{2}=\dfrac{1}{8}+\dfrac{1}{18}=\dfrac{9}{72}+\dfrac{4}{72}=\dfrac{13}{72}$
Donc :
\[O_{1}O_{2}=O_{1}I+IO_{2}\]Ceci prouve que les deux cercles sont tangents.

Les propriétés précédentes des cercles de Ford ont inspiré certains artistes. Voici une image de Jos Leys, artiste géomètre :

Cercles de Ford par Jos Leys

D’autres images sur le site de Jos Leys.

D) Approximation d'un réel

Pour finir, les élèves de la section ont découvert une application possible des suites de Farey : on souhaite encadrer le nombre $\dfrac{1}{\sqrt{2}}$ par des fractions dont le dénominateur ne dépasse pas 20. On commence par encadrer par deux termes consécutifs de $F_2$ : \[\dfrac{1}{2}<\dfrac{1}{\sqrt{2}}<\dfrac{1}{1}\] Ensuite, on calcule la fraction médiane de $\dfrac{1}{2}$ et $\dfrac{1}{1}$ : \[\dfrac{1+1}{2+1}=\dfrac{2}{3}\] Ainsi, à l’étape 2 : \[\dfrac{2}{3}<\dfrac{1}{\sqrt{2}}<\dfrac{1}{1}\] Etape 3 : \[\dfrac{2+1}{3+1}=\dfrac{3}{4}\] \[\dfrac{2}{3}<\dfrac{1}{\sqrt{2}}<\dfrac{3}{4}\] Finalement, après plusieurs étapes, on obtient l’encadrement voulu : \[\dfrac{12}{17}<\dfrac{1}{\sqrt{2}}<\dfrac{5}{7}\]

Voici un programme Scratch donnant un encadrement de $\dfrac{1}{\sqrt{n}}$ par des fractions dont le dénominateur ne dépasse pas $20$ :

Le programme Scratch à télécharger

Suite de Farey et cercles de Ford Lire la suite »

ChatGPT pour générer des questions

Laisser un commentaire /

Dans cet article, je vous explique comment générer un nombre important de questions très rapidement avec ChatGPT. L’exemple proposé est pour un import dans Moodle avec un fichier au format gift.

L’intérêt est de générer dans Moodle un test de 5 questions qui seront piochées aléatoirement parmi 20 questions. Ainsi, lorsque l’élève décide de refaire le test, les questions seront différentes. Les élèves de la classe auront également des questions différentes.

Pour cela, se connecter à ChatGPT : https://chatgpt.com/

Voici un exemple de requête:

Peux-tu me générer 15 questions au format réponse courte pour un import Moodle (code pour import dans un fichier gift) sur calculer une quatrième proportionnel dans un tableau : tu proposes 4 cases dans un tableau de proportionnalité, 3 cases à valeurs numériques et une avec une lettre. Il faut trouver la lettre.

Il faut ensuite affiner la requête pour modifier la rédaction de la question, la correction, certaines valeurs numériques… Le code fourni est à coller dans un fichier texte et à importer dans Moodle :

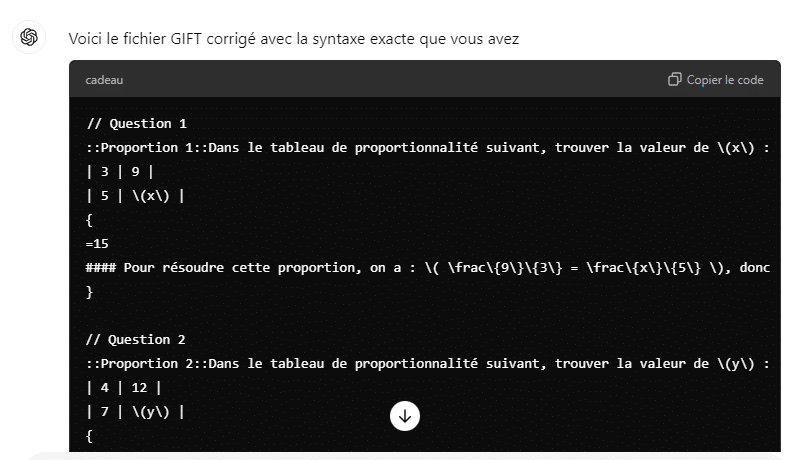
Ci-dessous, une image d’une des questions du test que verra l’élève :

Bien évidemment, une petite relecture s’impose. ChatGPT est encore capable de faire des erreurs de calcul. Pour les QCM, les distracteurs qu’il propose manquent souvent d’intérêt mais il est possible de lui faire rectifier.

En conclusion, ChatGPT peut être utile pour générer un nombre important d’exercices de base permettant de faire travailler la technique aux élèves. Il est capable d’adapter ses corrections et de jouer sur certaines variables didactiques (si on lui demande !). Oubliez le si vous souhaitez créer une véritable activité permettant d’introduire une nouvelle notion aux élèves…

 

 

 

 

ChatGPT pour générer des questions Lire la suite »

Questions flash

Laisser un commentaire /

Pour retravailler les évaluations nationales de 6e, 5e et 4e, les sections questions flash sont en développement.

Je les travaille en classe avec l’application Plickers. Pratique, ludique et très efficace, Plickers permet d’avoir une vue d’ensemble des résultats de ses élèves à une question posée.

Les documents proposés sont au format PDF. Ils peuvent être distribués aux élèves, projetés au tableau, ou retapés dans l’application Plickers. L’outil d’importation de questions doit faciliter le travail avec un simple copier-coller.

Plus d’informations ici : comment importer des questions dans Plickers

 

Questions flash Lire la suite »