Chapitre 13
Cône et volume
Chapitre 13 : Cône et volume
A) Représentation en perspective cavalière et patron
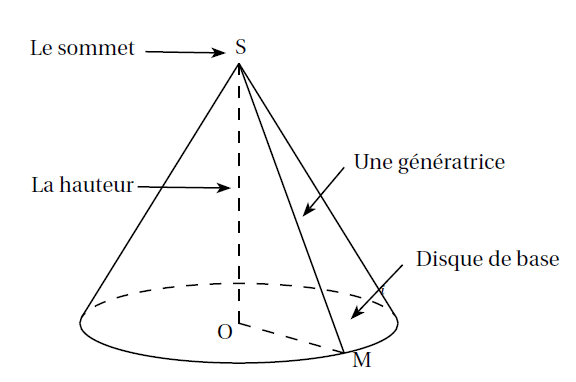
Définition : Un cône de révolution de sommet $S$ est le solide engendré par la rotation d’un triangle $SOM$ rectangle en $O$, autour de la droite $(SO)$.
- Le disque de centre $O$ et de rayon $[OM]$ est la base de ce cône.
- Le segment $[SM]$ est appelé une génératrice de ce cône.
- La hauteur de ce cône est le segment $[SO]$ (ou la longueur $SO$).
Exemple : Un cône de sommet $S$, de hauteur $[SO]$ et de base le disque de centre $O$ et de rayon $[OM]$.
Exemple : Pour construire le patron du cône ci-dessous, il faut calculer la mesure de l’angle $\widehat{M’SM}$.
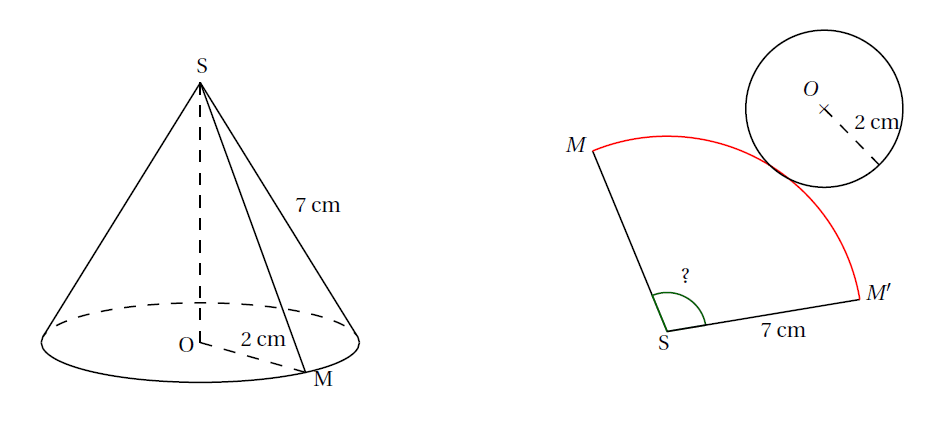
Longueur du cercle de centre $S$ et de rayon $7~\text{cm}$ :
\[2\times R\times \pi=2\times 7~\text{cm}\times \pi=14\pi~\text{cm}\]
La longueur de l’arc de cercle rouge est égale à la longueur du cercle de centre $O$ et de rayon $2~\text{cm}$ :
\[2\times R\times \pi=2\times 2~\text{cm}\times \pi=4\pi~\text{cm}\]
La longueur d’un arc de cercle est proportionnelle à la mesure de l’angle qui l’intercepte. Ainsi, pour calculer la mesure le l’angle $\widehat{M’SM}$, on utilise un tableau de proportionnalité :
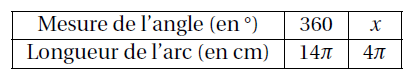
L’égalité des produits en croix permet d’écrire :
\[14\pi\times x=360\times 4\pi\]Ainsi :
\begin{eqnarray*}
x&=&\dfrac{360\times 4\pi}{14\pi}\\
x&\approx& 103
\end{eqnarray*}
L’angle $\widehat{M’SM}$ mesure environ $103°$.
B) Volume d'un cône
Propriété : Le volume d’un cône de hauteur $h$ et de base d’aire $B$ est donné par la formule :
\[V=\dfrac{\text{Aire}_{\text{base}}\times \text{hauteur}}{3}=\dfrac{B\times h}{3}\]
En notant $r$ le rayon de disque de base, on obtient :
\[V=\dfrac{\pi\times r^{2}\times h}{3}\]
Exemple : Calculer le volume, en $\text{cm}^{3}$, d’un cône de hauteur $8~\text{cm}$ et de rayon de base $6~\text{cm}$.
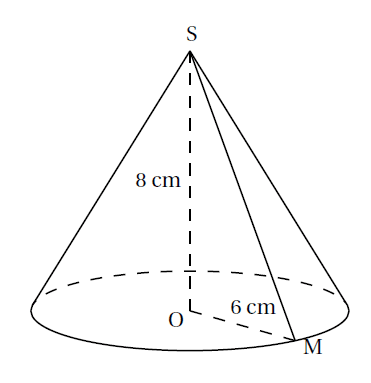
Donner une valeur approchée à l’unité près.
Valeur exacte en $\text{cm}^{3}$ du volume de ce cône :
\[V=\dfrac{\pi\times (6~\text{cm})^{2}\times 8~\text{cm}}{3}=96\pi~\text{cm}^{3}\]
Valeur approchée en $\text{cm}^{3}$ et à l’unité près :
\[V\approx 301~\text{cm}^{3}\]