Chapitre 2
Développer et réduire une expression littérale
Chapitre 2 : développer et réduire une expression littérale
Développer et réduire permet :
- de prouver que deux expressions littérales sont équivalentes ;
- de démontrer qu’une propriété est vraie.
A) Développer avec la distributivité
Propriétés : $k,a,b,c$ et $d$ sont des nombres relatifs quelconques :
\begin{eqnarray*}
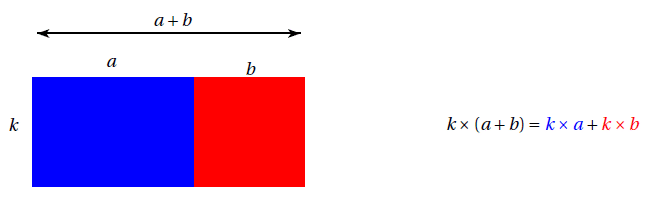
k \times (a+b)&=&k\times a + k\times b \\
&&\\
(a+b)\times (c+d)&=&a\times c + a\times d + b\times c + b\times d\\
\end{eqnarray*}
Interprétation géométrique :
\begin{eqnarray*}
A&=&-3x(4x-6)\\
A&=&-12x^{2}+18x\\
\end{eqnarray*}
B) Développer avec les identités remarquables
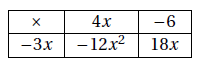
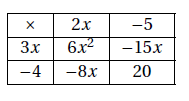
Propriétés : $a$ et $b$ désignent des nombres relatifs :
- $ (a+b)^{2}=a^{2}+2\times a\times b+b^{2}=a^{2}+2ab+b^{2}$
- $ (a-b)^{2}=a^{2}-2\times a\times b+b^{2}=a^{2}-2ab+b^{2}$
- $ (a+b)(a-b)=a^{2}-b^{2} $
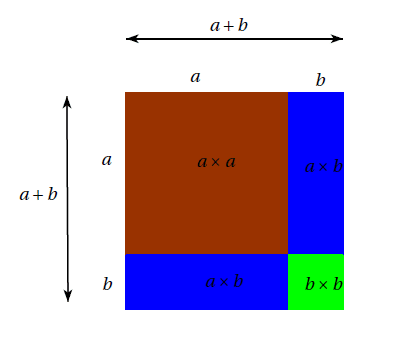
Interprétation géométrique : Pour calculer l’aire du carré, on peut procéder de deux manières :
- $A=(a+b)(a+b)=(a+b)^{2}$
- $A=a^{2}+ab+ab+b^{2}=a^{2}+2ab+b^{2}$
On en a déduit : $(a+b)^{2}=a^{2}+2ab+b^{2}$.
Démonstration : Démontrons la première identité remarquable :
\begin{eqnarray*}
(a+b)^{2}&=&(a+b)(a+b)\\
&=&a\times a+a\times b+b\times a+b\times b\\
&=&a^{2}+a\times b+a\times b+b^{2}\\
&=&a^{2}+2\times a\times b+b^{2}\\
&=&a^{2}+2ab+b^{2}
\end{eqnarray*}
Exemples : Les identités remarquables permettent de développer plus rapidement une expression :
\begin{eqnarray*}
A&=&(2x+5)^{2}\\
A&=&(2x)^{2}+2\times 2x\times 5+5^{2}\\
A&=&4x^{2}+20x+25\\
\end{eqnarray*}
\begin{eqnarray*}
B&=&(x-6)^{2}\\
B&=&x^{2}-2\times x\times 6+6^{2}\\
B&=&x^{2}-12x+36\\
\end{eqnarray*}
\begin{eqnarray*}
C&=&(3x-4)(3x+4)\\
C&=&(3x)^{2}-4^{2}\\
C&=&9x^{2}-16
\end{eqnarray*}
Exemples : Les identités remarquables peuvent servir pour calculer mentalement :
- $99\times 101=(100-1)(100+1)=100^{2}-1^{2}=10~000-1=9~999$
- $29^{2}=(30-1)^{2}=30^{2}-2\times 30\times 1
+1^{2}=900-60+1=841$
C) Le calcul littéral pour démontrer
Exemple : Les programmes de calcul ci-dessous sont-ils équivalents ?
- Choisir un nombre
- Ajouter 7
- Ajouter le nombre de départ
- Choisir un nombre
- Multiplier le résultat par 2
- Ajouter 10
- Retrancher 3
Choisissons $x$ pour remplacer le nombre de départ :
- $x$
- $x+7$
- $x+7+x=2x+7$
- $x$
- $2\times x$
- $2\times x+10$
- $2\times x+10-3=2x+7$
Exemples :
- Si $n$ désigne un nombre entier, on peut traduire la formulation “être la somme de deux entiers consécutifs” par l’expression littérale : $n+(n+1)$.
- Si $n$ désigne un nombre entier, on peut traduire la formulation “être un multiple de 3” par l’expression littérale : $3\times n=3n$.
- Si $n$ désigne un nombre entier, on peut traduire la formulation “être un nombre pair” par l’expression littérale : $2\times n=2n$.
- Si $n$ désigne un nombre entier, on peut traduire la formulation “être un nombre impair” par l’expression littérale : $2\times n+1=2n+1$.
Exemple : Montrer que pour n’importe quel nombre entier $n$, $(n+1)^{2}-(n-1)^{2}$ est un multiple de 4.
\begin{eqnarray*}
(n+1)^{2}-(n-1)^{2}&=&[n^{2}+2\times n\times 1+1^{2}]-[n^{2}-2\times n\times 1+1^{2}]\\
&=&[n^{2}+2n+1]-[n^{2}-2n+1]\\
&=&n^{2}+2n+1-n^{2}+2n-1\\
&=&4n
\end{eqnarray*}
Donc pour tout nombre entier $n$, $(n+1)^{2}-(n-1)^{2}$ est bien un multiple de 4.