Chapitre 20
La double distributivité
Chapitre 20 : La double distributivité
Propriété : $a$,$b$, $c$ et $d$ sont des nombres relatifs quelconques :
Démonstration :
$(a+b)(c+d)=(a+b)\times c+(a+b)\times d=a\times c+b\times c+a\times d+b\times d=a\times c+a\times d+b\times c+b\times d$
Exemples :
\begin{eqnarray*}
A&=&(3+2x)(x+4)\\
A&=&3\times x+3\times 4+2x\times x+2x\times 4\\
A&=&3x+12+2x^{2}+8x\\
A&=&2x^{2}+11x+12
\end{eqnarray*}
\begin{eqnarray*}
B&=&(2x-5)(3x-4)\\
B&=&(2x+(-5))(3x+(-4))\\
B&=&2x\times 3x+2x\times (-4)+(-5)\times 3x+(-5)\times (-4)\\
B&=&6x^{2}+(-8x)+(-15x)+20\\
B&=&6x^{2}-23x+20\\
\end{eqnarray*}
Interprétation géométrique :
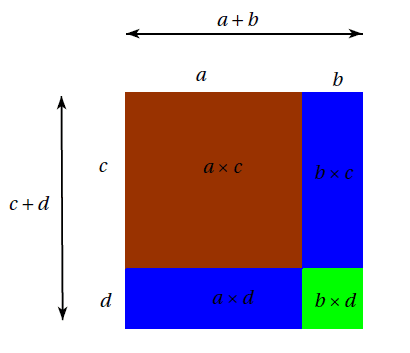
Exemples : avec une rédaction permettant d’aller plus vite…
\begin{eqnarray*}
B&=&(2x-5)(3x-4)\\
B&=&2x\times 3x-2x\times 4-5\times 3x+5\times 4\\
B&=&6x^{2}-8x-15x+20\\
B&=&6x^{2}-23x+20\\
\end{eqnarray*}
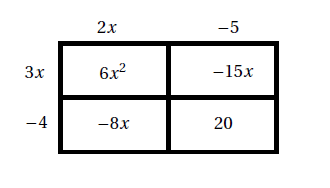
\begin{eqnarray*}
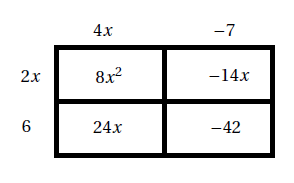
C&=&(4x-7)(2x+6)-2(3x-4)\\
C&=&4x\times 2x+4x\times 6-7\times 2x-7\times 6-2\times 3x+2\times 4\\
C&=&8x^{2}+24x-14x-42-6x+8\\
C&=&8x^{2}+4x-34\\
\end{eqnarray*}