Chapitre 4
Probabilités
Chapitre 4 : Probabilités
A) Notion d’événement
Définition : Un événement est constitué par certaines issues d’une expérience aléatoire. On dit que chacune de ces issues réalise l’événement.
Exemple : On fait tourner la roue de loterie ci-dessous pour gagner un lot.
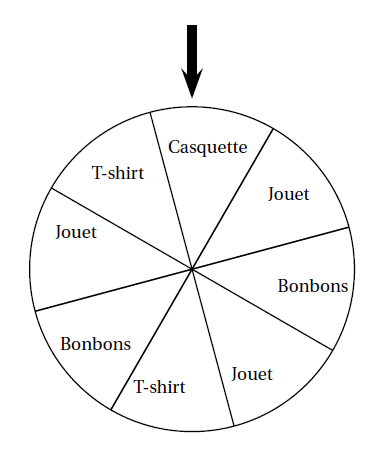
Les issues de l’expérience sont : gagner une casquette, gagner des bonbons, gagner un jouet, gagner un T-shirt.
L’événement A : « Gagner un vêtement » est constitué de deux issues : gagner une casquette et gagner un T-shirt.
B) Probabilité d’un événement
Définition : La probabilité d’un événement est égale au quotient de nombre d’issues favorables (issues dans lesquelles on obtient le résultat) par le nombre total d’issues possibles.
Propriétés :
- La probabilité d’un événement est un nombre compris entre $0$ et $1$.
- La somme des probabilités des issues d’une expérience aléatoire est égale à $1$.
Exemple : On tire au hasard une carte dans un jeu de $32$ cartes. La probabilité de l’événement « La carte tiré est un Coeur » est $\dfrac{8}{32}$. En effet, il y a $8$ coeurs sur $32$ cartes au total.
Remarques : Une probabilité peut s’exprimer sous diverses formes (décimale, fractionnaire, pourcentage).
Propriétés :
- La probabilité d’un événement qui se produit nécessairement (événement certain) est égale à $1$.
- La probabilité d’un événement qui ne peut pas se produire (événement impossible) est égale à $0$.
C) Événements incompatibles et événements contraires
Définition : Deux événements sont incompatibles s’ils ne peuvent pas se réaliser en même temps.
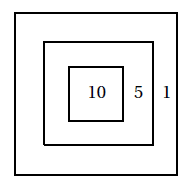La probabilité relative à une région est le rapport de son aire à celle de la cible.
Pour calculer la probabilité qu’il gagne au moins $5$ points, on peut calculer la probabilité des événements incompatibles « gagner $5$ points » et « gagner $10$ points » :
- Probabilité de gagner $5$ points : \[\dfrac{2a\times 2a-a\times a}{3a\times 3a}=\dfrac{4a^{2}-a^{2}}{9a^{2}}=\dfrac{3a^{2}}{9a^{2}}=\dfrac{3}{9}\]
- Probabilité de gagner $10$ points : \[\dfrac{a\times a}{3a\times 3a}=\dfrac{a^{2}}{9a^{2}}=\dfrac{1}{9}\]
- De manière intuitive, on additionne les probabilités précédentes pour obtenir la probabilité de gagner au moins $5$ points : \[\dfrac{3}{9}+\dfrac{1}{9}=\dfrac{4}{9}\]
Propriété : Si deux événements sont incompatibles, la probabilité que l’un ou l’autre se réalise est égale à la somme de leurs probabilités.
Définition : L’événement contraire d’un événement est celui qui se réalise lorsque l’événement n’a pas lieu.
Propriété : La somme d’un événement et de son contraire est égale à $1$.
Démonstration : Un événement et son contraire sont incompatibles et la réalisation de l’un ou de l’autre est certaine. Donc la somme de leur probabilité est égale à 1.
Exemple : Retour à l’exemple précédent.
N’y a-t-il pas un moyen plus rapide de calculer la probabilité que le joueur gagne au moins $5$ points ?
On peut calculer l’événement contraire de « gagner au moins $5$ points » c’est à dire « gagner $1$ point » :
\[\dfrac{3a\times 3a-2a\times 2a}{3a\times 3a}=\dfrac{9a^{2}-4a^{2}}{9a^{2}}=\dfrac{5}{9}\]
La somme de ces $2$ événements contraires étant égale à $1$, on en déduit :
\[\dfrac{5}{9}+?=1~(\text{ou}~\dfrac{9}{9})\]
La probabilité que le joueur gagne au moins $5$ points est de $\dfrac{4}{9}$.