Chapitre 5
L'inégalité triangulaire
Chapitre 5 : L'inégalité triangulaire
Propriété : Dans un triangle, la somme des longueurs de deux côtés est supérieure à la longueur du troisième côté.
Exemple : Dans un triangle $ABC$, on a :
\[AC+CB>\textcolor{blue}{AB}\]
\[AB+BC>\textcolor{green}{AC}\]
\[BA+AC>\textcolor{red}{BC}\]
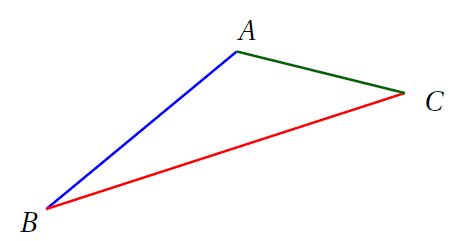
Conséquence : Cela signifie que pour pouvoir construire un triangle dont on donne les longueurs des trois côtés, il suffit de vérifier que la somme des deux plus petites longueurs est supérieure à la troisième.
Exemples :
- Peut-on construire un triangle $ABC$ tel que $AB = 8~\text{cm}$, $AC =4~\text{cm}$ et $BC = 2~\text{cm}$ ?
$AC +BC = 4~\text{cm}+2~\text{cm}= 6~\text{cm}$ et $AB = 8~\text{cm}$.
Donc $AC +BC < AB$ et on ne peut donc pas construire le triangle $ABC$. - Peut-on construire un triangle $EFG$ tel que $EF = 7,2~\text{cm}$, $EG = 4,5~\text{cm}$ et $FG = 3,3~\text{cm}$ ?
$EG +GF = 4,5~\text{cm}+3,3~\text{cm}= 7,8~\text{cm}$ et $EF = 7,2~\text{cm}$. Donc $EG +GF > EF$ et on peut construire le triangle $EFG$.
Propriétés :
- Si un point $B$ appartient à un segment $[AC]$ alors $\textcolor{red}{AB} + \textcolor{green}{BC} = AC$.
- Si $A$, $B$, $C$ sont trois points tels que $\textcolor{red}{AB} + \textcolor{green}{BC} = AC$ alors le point $B$ appartient au segment $[AC]$.
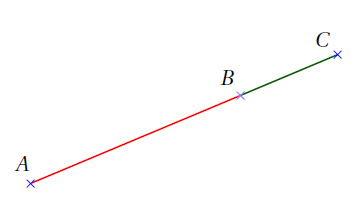
Bilan : Dans ce chapitre, je dois savoir :
- Utiliser l’inégalité triangulaire pour justifier qu’un triangle est constructible ou non.
- Construire des triangles dont on connaît les longueurs des 3 côtés.
- Construire un triangle en respectant une échelle.