Chapitre 5
Notion de fonction
Chapitre 5 : Notion de fonction
A) Introduction
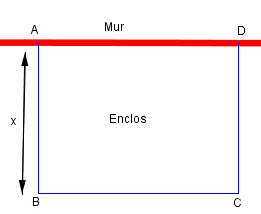
Mathilde veut construire un petit enclos rectangulaire pour son lapin. Son papi lui fournit 6,5 m de grillage.
En plaçant l’enclos contre le mur de son jardin, le grillage ne délimitera que trois côtés. Mathilde place un premier poteau A contre le mur. Elle veut déterminer à quelle distance $x$ placer le poteau B pour que la surface de l’enclos soit maximale.
Dans l’activité de ce chapitre nous avons associé à la longueur $x$ (distance du point B au mur) la surface de l’enclos. Ce procédé s’est traduit ainsi :
\[x\longmapsto x(6,5-2x)\]
B) Définition et vocabulaire
Définition : Une fonction numérique $f$ est un procédé de calcul qui, à tout nombre $x$, associe le nombre $f(x)$ (lire « $f$ de $x$ »).
On note : \[f:x\longmapsto f(x)\]
- $f$ est la fonction qui, à un nombre $x$, fait correspondre son double : \[f:x\longmapsto 2x\] \[f(x)=2x\]
- $g$ est la fonction qui, à un nombre $x$, fait correspondre son carré : \[g:x\longmapsto x^{2}\] \[g(x)=x^{2}\]
- $h$ est la fonction qui, à un nombre $x$, associe son carré augmenté de 1 : \[h:x\longmapsto x^{2}+1\] \[h(x)=x^{2}+1\]
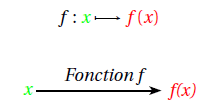
Exemple : Soit le programme de calcul ci-dessous. Déterminer l’expression algébrique de la fonction $f$ associée à ce programme de calcul.
- Choisir un nombre
- Retrancher 5
- Multiplier le résultat par 4
- Je choisis $x$
- $x-5$
- $(x-5)\times 4$
Donc : $f(x)=4(x-5)$.
- $f(x)$ est l’image de $x$ par la fonction $f$.
- $x$ est un antécédent de $f(x)$ par la fonction $f$.
Remarque : Un nombre peut avoir plusieurs antécédents mais chaque nombre a au plus une image.
Exemple : Dans l’activité, nous avons trouvé à l’aide d’un tableur que si $x=1,6$, l’aire de l’enclos était maximale. Ainsi au nombre 1,6 nous associons le nombre 5,28. Nous pourrons écrire que :
\[f(1,6)=5,28\]Nous pouvons dire que :
- 5,28 est l’image de 1,6 par la fonction $f$.
- 1,6 est un antécédent de 5,28 par la fonction $f$.
Exemple : Soit $f$ la fonction définie par $f:x\longmapsto x^{2}-3$.
- Calculer l’image de 2 par la fonction $f$.
\begin{eqnarray*}
f(2)&=&2^{2}-3\\
&=&4-3\\
&=&1\\
\end{eqnarray*}
L’image de 2 par la fonction $f$ est 1.
- Prouver que 5 est un antécédent de 22 par la fonction $f$.
\begin{eqnarray*}
f(5)&=&5^{2}-3\\
&=&25-3\\
&=&22\\
\end{eqnarray*}
Un antécédent de 22 par la fonction $f$ est 5.
Exemple : Ce tableau définit une fonction $f$ qui à chaque nombre de la 1ère ligne associe un nombre de la 2ème ligne.
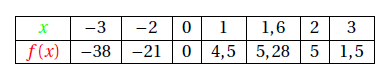
D’après le tableau :
- L’image de -2 par la fonction $f$ est -21 : $f(-2)=-21$.
- L’antécédent de 4,5 par la fonction $f$ est 1: $f(1)=4,5$
C) Représentation graphique d'une fonction
Définition : La courbe représentative d’une fonction $f$ est l’ensemble des points dont les coordonnées sont de la forme $(x ;f(x))$.
Exemple : Voici la représentation graphique de la fonction $f$ de l’activité ($f(x)=x(6,5-2x)$) :
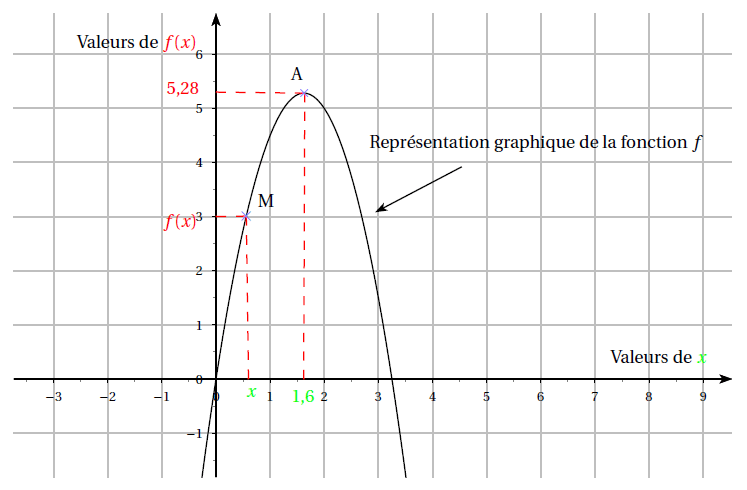
Par lecture graphique :
- On constate que l’aire est maximale pour $x\approx 1,6$. Cette aire maximale vaut environ 5,28 m$^{2}$.
- On retrouve ainsi que l’image de 1,6 par la fonction $f$ est égale à 5,28.
- On remarque également qu’un nombre peut avoir plusieurs antécédents : les antécédents de 4 par la fonction $f$ sont environ 0,8 et 2,5.