Chapitre 25
Quadrilatères particuliers et axes de symétrie
Chapitre 25 : Quadrilatères particuliers et axes de symétrie
A) Losange
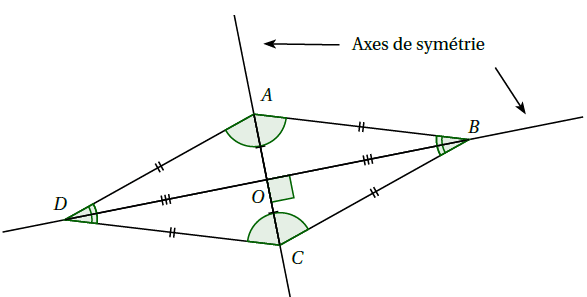
Définition : Un losange est un quadrilatère qui a 4 côtés de même longueur.
Propriétés :
- Un losange a deux axes de symétrie : ses diagonales.
- Un losange a ses angles opposés 2 à 2 de même mesure.
- Un losange a ses diagonales qui se coupent en leur milieu et qui sont perpendiculaires.
Exemple : Dans le losange $ABCD$ :
- Les droites $(d_{1})$, $(d_{2})$, $(RT)$ et $(US)$ sont les axes de symétrie.
- $J$ est le milieu de $[RT]$ et de $[SU]$.
- $RT=SU$ et $(RT)$ est perpendiculaire à $(SU)$.
B) Rectangle
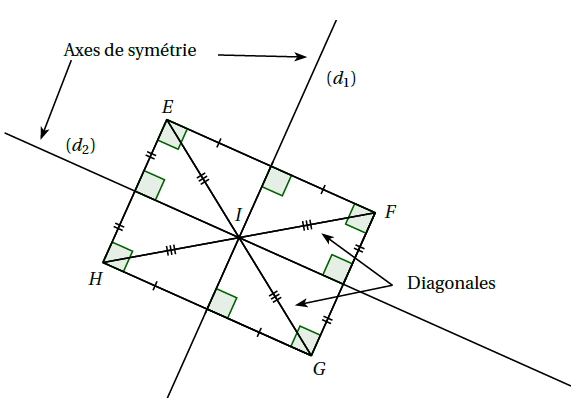
Définition : Un rectangle est un quadrilatère qui a 4 angles droites.
Propriétés :
- Un rectangle a deux axes de symétrie : les médiatrices de ses côtés.
- Un rectangle a ses diagonales qui se coupent en leur milieu et ont la même longueur.
- Un rectangle a des côtés opposés de même longueur et parallèles.
Exemple : Dans le rectangle $EFGH$ :
- Les droites $(d_{1})$ et $(d_{2})$ sont les axes de symétrie.
- $I$ est le milieu de $[EG]$ et de $[FH]$.
- $EG=HF$.
- $EF=GH$ et $EH=GF$.
C) Carré
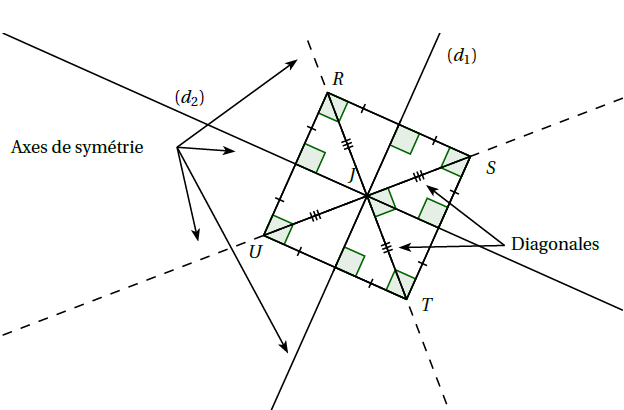
Définition : Un carré est un quadrilatère qui a 4 angles droites et 4 côtés de même longueur.
Remarque : Un carré est à la fois un losange (il a quatre côtés de même longueur) et un rectangle (il a quatre angles
droits).
Propriétés :
- Un carré a quatre axes de symétrie : ses diagonales et les médiatrices de ses côtés.
- Un carré a ses côtés opposés deux à deux parallèles.
- Un carré a ses diagonales qui se coupent en leur milieu, qui sont perpendiculaires et qui ont la même longueur.
Exemple : Dans le carré $RSTU$ :
- Les droites $(d_{1})$, $(d_{2})$, $(RT)$ et $(US)$ sont les axes de symétrie.
- $J$ est le milieu de $[RT]$ et de $[SU]$.
- $RT=SU$ et $(RT)$ est perpendiculaire à $(SU)$.
D) Parallélogramme
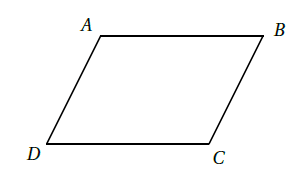
Définition : Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
Exemple : Le quadrilatère $ABCD$ ci-dessous est un parallélogramme. Ses côtés opposés sont parallèles:\\
$(AB)//(DC)$ et $(AD)//(BC)$.
Remarques :
- Un parallélogramme ne possède pas d’axe de symétrie.
- Un rectangle est un parallélogramme qui a un angle droit.
- Un losange est un parallélogramme qui a deux côtés consécutifs de même longueur.