Chapitre 8
Réciproque du théorème de Pythagore
Chapitre 8 : Réciproque du théorème de Pythagore
Propriété (Réciproque du théorème de Pythagore) : Si le carré de la longueur du plus grand côté d’un triangle est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle.
Remarque : Cette propriété permet de prouver qu’un triangle est rectangle ou non.
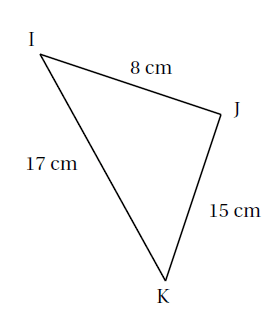
Exemple : Le triangle
Ainsi, l’égalité de Pythagore est vérifiée donc le triangle
Propriété : Si le carré de la longueur du plus grand côté d’un triangle n’est pas égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle n’est pas rectangle.
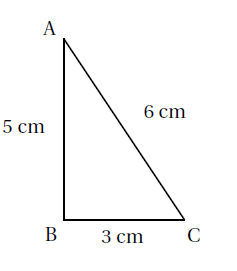
Exemple : Le triangle
Ainsi, l’égalité de Pythagore n’est pas vérifiée donc le triangle