
Propriété : $ABC$ est un triangle.
Si les points $M$ et $N$ sont des points respectifs des demi-droites $[AB)$ et $[AC)$ tels que les droites $(BC)$ et $(MN)$ sont parallèles, alors :
\[\dfrac{A\textcolor{red}{M}}{A\textcolor{blue}{B}}=\dfrac{A\textcolor{red}{N}}{A\textcolor{blue}{C}}=\dfrac{\textcolor{red}{MN}}{\textcolor{blue}{BC}}\]
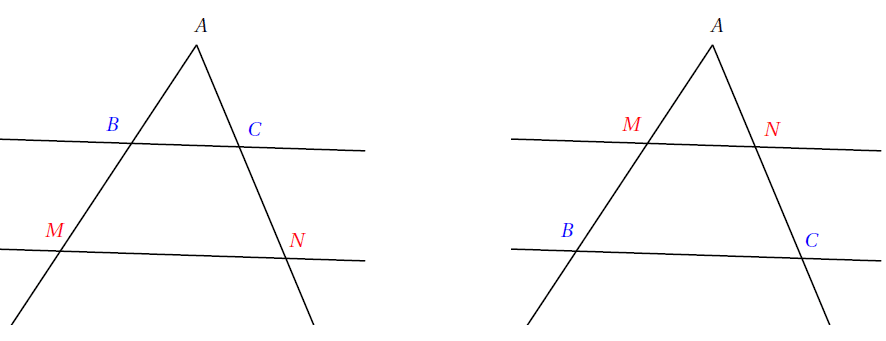
Démonstration : Les droites $(BC)$ et $(MN)$ étant parallèles, les angles correspondants $\widehat{ABC}$ et $\widehat{AMN}$ et les angles correspondants $\widehat{ACB}$ et $\widehat{ANM}$ ont la même mesure.
Ainsi, les triangles $ABC$ et $AMN$ ont leurs angles deux à deux de même mesure (on dit que les deux triangles sont semblables).
Donc le triangle $ABC$ est un agrandissement (ou une réduction) du triangle $AMN$. On obtient donc les longueurs des côtés d’un des triangles en multipliant par un nombre non nul les longueurs des côtés de l’autre triangle. Ceci revient à dire que le tableau ci-dessous est un tableau de proportionnalité :
On peut alors écrire les égalités suivantes :
\[\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\]

Exemple : Soit un triangle tel que $AC = 7$ cm, $AB = 2,5$ cm et $BC = 8$ cm.
Soit $M$ un point appartenant au segment $[AB]$ tel que $AM = 1,7$ cm et $N$ le point d’intersection de la droite $(BC)$ avec la parallèle à $(AC)$ passant par $M$.
Calculer $BN$.
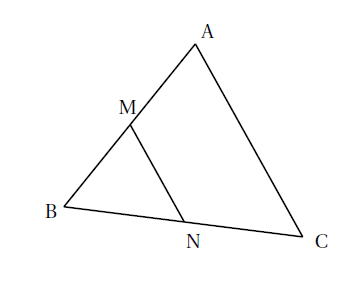 $M\in [AB]$
$M\in [AB]$
$N\in [BC]$
Les droites $(MN)$ et $(AC)$ sont parallèles.
D’après le théorème de Thalès :
\[\dfrac{BM}{BA}=\dfrac{BN}{BC}=\dfrac{MN}{AC}\]
\[\dfrac{0,8}{2,5}=\dfrac{BN}{8}=\dfrac{MN}{7}\]
Donc :
\[\dfrac{0,8}{2,5}=\dfrac{BN}{8}\]
Ainsi :
\[BN=\dfrac{0,8\times 8}{2,5}=2,56~\text{cm}\]
Propriété : $ABC$ est un triangle.
Si les points $M$ et $N$ sont des points respectifs des demi-droites $[AB)$ et $[AC)$ tels que $\dfrac{A\textcolor{red}{M}}{A\textcolor{blue}{B}}\neq \dfrac{A\textcolor{red}{N}}{A\textcolor{blue}{C}} $ alors les droites $(BC)$ et $(MN)$ ne sont pas parallèles.
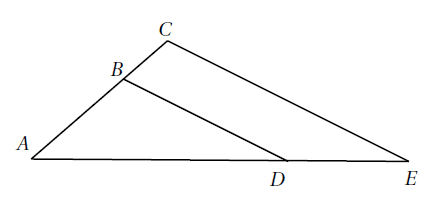
Exemple : On donne les longueurs suivantes :
$AB = 6,3$ cm ; $BC = 4,9$ cm ; $AE = 17$ cm et $DE = 7$ cm.
Les droites $(BD)$ et $(CE)$ sont-elles parallèles ? Justifier la réponse.
\[
\left.
\begin{array}{ccccc}
\dfrac{AB}{AC}&=&\dfrac{6,3}{11,2}&=&\dfrac{9}{16}\\
\\
\dfrac{AD}{AE}&=&\dfrac{10}{17}&
\end{array}
\right\}\mbox{Donc}~~\dfrac{AB}{AC}\neq \dfrac{AD}{AE}
\]Donc les droites $(BD)$ et $(CE)$ ne sont pas parallèles.
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |