Chapitre 3
Statistiques et tableur
Chapitre 3 : Statistiques et tableur
A) Fréquence
Définition : La fréquence est le quotient (ou rapport) de l’effectif de cette valeur sur l’effectif total de la population :
\[\text{Fréquence}=\dfrac{\text{Effectif}}{\text{Effectif total}}\]
Exemple : Dans un collège de 450 élèves, 110 élèves ont trois frères et soeurs. La fréquence des élèves ayant trois frères et soeurs est égale à :
\[\text{Fréquence}=\dfrac{110}{450}\approx 0,244\]En pourcentage, cette fréquence vaut environ 24,4 %.
B) Moyenne d'une série statistiques
Définition : La moyenne pondérée d’une série de valeurs est le nombre obtenu :
- en additionnant toutes les valeurs de la série ;
- en divisant cette somme par l’effectif total de la série.
Exemple : On a relevé les distances (en km) parcourues par un commercial au cours de ses $7$ derniers jours travaillés. On peut calculer la distance moyenne journalière de deux manières différentes :
- Avec un tableur :
En A9, on tape la formule : =MOYENNE(A2: A8) - A la main :
\[\dfrac{374~\text{km}+475~\text{km}+326~\text{km}+408~\text{km}+372~\text{km}+431
~\text{km}+274~\text{km}}{7}=380~\text{km}\]La distance moyenne journalière parcourue par ce commercial est égales à $380~\text{km}$.
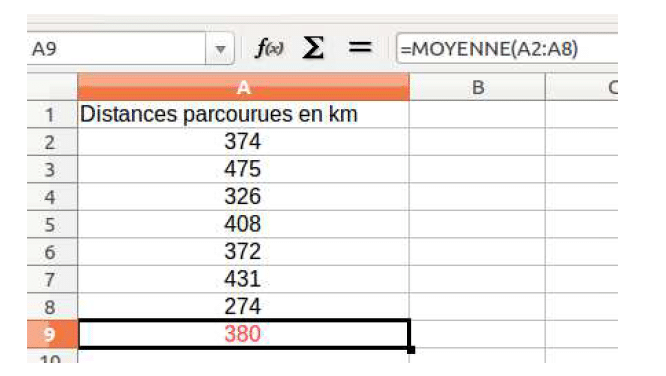
Interprétation : Si ce commercial avait parcouru le même nombre de kilomètres chaque jour, celui-ci serait de $380$ km.
Remarque : Le tableur permet de traiter des données réelles en grand nombre en s’affranchissant de calculs fastidieux.
Exemple : A un concours scientifique, les mathématiques ont un coefficient 5, la physique un coefficient 3 et la géologie un coefficient 2. Carine a obtenu 11 en mathématiques, 9 en physique et 12 en géologie.
Quelle est la moyenne de Carine à ce concours ?
\[\text{Moyenne}=\dfrac{11\times 5+9\times 3+12\times 2}{5+3+2}=10,6\]
C) Médiane d'une série statistiques
Définition : Les valeurs d’une série statistique étant rangées par ordre croissant (ou décroissant), la médiane est un nombre M tel que :
- au moins la moitié des valeurs de la série sont inférieures ou égales à M ;
- au moins la moitié des valeurs de la série sont supérieures ou égales à M.
Exemple : (Effectif total impair)
Calculer la médiane de la série suivante :
\[6-15-26-14-30-21-18-9-13\]
Je range les valeurs de la série dans l’ordre croissant :
\[6-9-13-14-15-18-21-26-30\]Je calcule l’effectif total : $9$
$9\div 2=4,5$ donc la médiane est la 5ème valeur : $M=15$
Il y a $5$ valeurs inférieures ou égales à la médiane et $5$ valeurs supérieures ou égales à la médiane.
Exemple : (Effectif total pair)
Calculer la médiane de la série suivante :
\[16-4-2-12-9-15-17-1\]
Je range les valeurs de la série dans l’ordre croissant :
\[1-2-4-9-12-15-16-17\]Je calcule l’effectif total : $8$
$8\div 2=4$ donc la médiane est la moyenne des 4ème et 5ème valeurs :
\[M = \dfrac{9+12}{2}=10,5\]Il y a $5$ valeurs inférieures ou égales à la médiane et $5$ valeurs supérieures ou égales à la médiane.
Exemple : Calculer la médiane de la série des lancers de javelot ci-dessous.
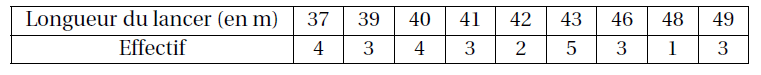
On peut calculer la médiane de deux manières différentes :
- Avec le tableur :
En H4, on tape la formule : =MEDIANE(A1: G4) - A la main :
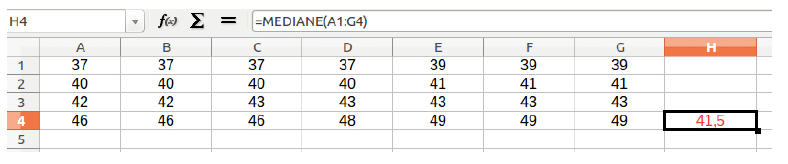
L’effectif total est $28$.
$28$ est pair donc la médiane est la moyenne des 14ème et 15ème longueurs. Elles sont égales à $41~\text{m}$ et $42~\text{m}$.
\[M= \dfrac{41~\text{m}+42~\text{m}}{2}=41,5~\text{m}\]La médiane est $41,5~\text{m}$.