Chapitre 17
La réciproque du théorème de Thalès
Chapitre 17 : La réciproque du théorème de Thalès
Propriété : Si deux droites $(AB)$ et $(AC)$ sont sécantes en un point $A$,
si les points $A, M, B$ et les points $A, N, C$ sont alignés dans le même ordre, et si $ \dfrac{AM}{AB}=\dfrac{AN}{AC} $ alors les droites $(BC)$ et $(MN)$ sont parallèles.
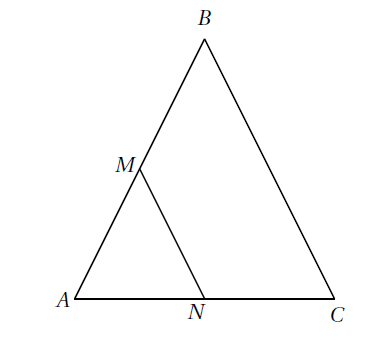
Remarque : Ce théorème permet de prouver que deux droites sont parallèles.
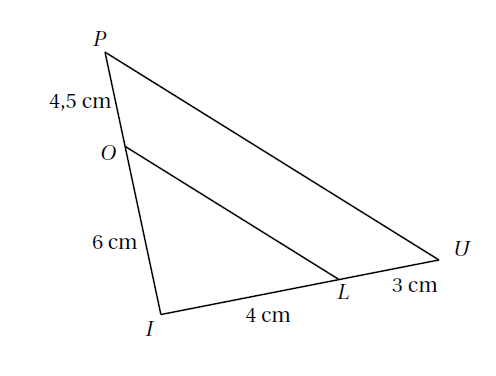
Exemple : Avec les données de la figure ci-dessous, démontrer que $(OL)$ est parallèle à $(UP)$.
\[
\left.
\begin{array}{ccccc}
\dfrac{IO}{IP}&=&\dfrac{6}{10,5}&=&\dfrac{4}{7}\\
\\
\dfrac{IL}{IU}&=&\dfrac{4}{7}&&\\
\end{array}
\right\}\mbox{Donc}~~\dfrac{IO}{IP}=\dfrac{IL}{IU}
\]- Les droites $(IP)$ et $(IU)$ sont sécantes en $I$.
- Les points $I, O, P$ et $I,L,U$ sont alignés dans le même ordre.
D’après la réciproque du théorème de Thalès, on en déduit que $(OL)$ est parallèle à $(UP)$.