Section d'excellence

Cryptographie

Cours de mathématiques de 4ème
Pour passer un message secret, on peut utiliser les acrostiches c’est à dire un poème ou strophe où les initiales de chaque vers, lues dans le sens vertical, composent un nom ou un mot-clé.

A) Les acrostiches

Pour passer un message secret, on peut utiliser les acrostiches c’est à dire un poème ou strophe où les initiales de chaque vers, lues dans le sens vertical, composent un nom ou un mot-clé. Dans le texte ci-dessous, la première lettre de chaque phrase donne le message caché : “codes secrets”.

acrostiche

Hergé utilise un procédé comparable dans le lotus bleu. Tintin y capte par radio le message à priori incompréhensible suivant :
“entre voie yokohama ns maison r charles andre dimanche seul aligner écran ou tentures serpent marchera inévitablement e proche occident halte intrus e “”.
Tintin finit par trouver la clef pour décoder ce message. Comment s’y prend-il ?

B) Le code de César

La substitution consiste à remplacer chaque lettre du texte clair par une lettre, un signe ou un nombre. La méthode la plus connue est le code de César. Plus précisément, son code consistait à décaler les lettres d’une façon convenue à l’avance.
Exemple : Le texte codé s’obtient en remplaçant chaque lettre du texte clair par la lettre qui est située trois rangs plus loin dans l’alphabet. La longueur du décalage constitue la clé du chiffrement.

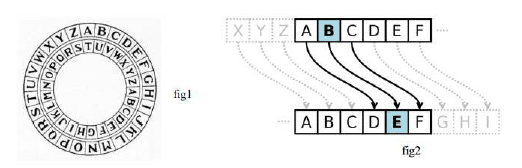
Code César

Par exemple, avec une clé de cryptage égale à 3 (fig 2) le mot CHAMPION est codé par FKDPSLRQ.
  1. Avec la même clé de cryptage, crypter votre prénom et décrypter le mot PDWKHPDWLTXHV.
  2. Décrypter le texte suivant sachant que la clé de codage est 10 :  LSOXFOXEOKEMYVVOQOGSVVIBYXSC
  3. Le texte en clair suivant RENDEZ-VOUS AU CDI donne : WJSIJEATZXFZHIN. Déterminer la clé de cryptage.
  4. Décrypter le texte suivant en supposant que le mot “ENNEMI” y figure : 
    STYWJJSSJRNIJYTZOTZWXJXYIJWJYTZW

C) Le cryptage affine

Un cryptage affine consiste à chiffrer chaque lettre de l’alphabet, puis à remplacer le nombre initial $x$ par le nombre $y$ qui est le reste de la division euclidienne de $ax+b$ par $26$. Les nombres $a$ et $b$ sont des entiers naturels qui forment la clé du cryptage. Dans le tableau ci-dessous, la clé de cryptage est $(3;7)$ (cela signifie que $a=3$ et $b=7$) :
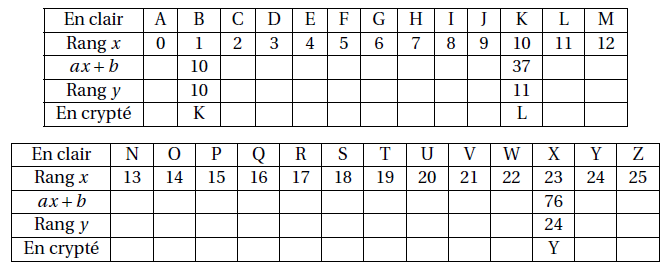
tableau cryptage affine
  1. Compléter le tableau puis coder votre prénom avec la clé $(3;7)$.
  2. Décrypter la phrase OT MGTJXG JT MGXPST NHNCT QHUJ OT NQF QP NXOOTZT avec la clé $(3;7)$.
  3. On prend maintenant pour clé $(5;13)$. Coder alors la phrase : Le théorème de Pythagore permet de calculer des longueurs dans un triangle rectangle.
  4. A vous de jouer : coder un message secret en utilisant le cryptage affine et en communiquant la clé permettant de le déchiffrer.

C) Le carré de Polybe

Polybe (200 – 155 ans avant Jésus-Christ environ) était un général reconnu de son temps. Il écrivit un traité de stratégie, dans lequel on trouve le système de transcription de signaux connu de nos jours sous son nom. Dans le carré de Polybe présenté ci-dessous, chaque lettre (sauf J qui est confondu à I) est repérée par un couple de nombres. Par exemple, M est codé par le couple $(3 ; 2)$, 3 étant la ligne de M dans le carré et 2, sa colonne :

Avec le carré ci-dessus, le mot maths se coderait 3211442343.

Le carré de Polybe permet alors de chiffrer si on le remplit dans un ordre différent. Pour le réaliser, le plus simple est d’utiliser une phrase assez longue, mais facile à retenir, comme “Le collège Willy Ronis est proche des bords de marne”. Pour remplir le carré, on écrit la phrase dans l’ordre en commençant en haut à gauche et en sautant les lettres déjà écrites. On complète ensuite par les lettres manquantes, toujours dans l’ordre :

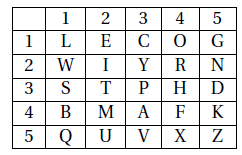
carré de Polybe

Deux élèves du collège Willy Ronis utilisent la phrase simple (” Le collège Willy Ronis est proche des bords de marne “) et le carré de Polybe ci-dessus pour communiquer par message codé.

  1. Quel message doit envoyer le premier élève afin de coder les phrases suivantes : La somme de deux nombres pairs est paire. La somme de deux nombres impairs est-elle paire ou impaire ? Quel message codé doit envoyer le deuxième élève afin de répondre à la question posée
  2. Deux enseignants du collège préparent le brevet blanc et communiquent par message codé en utilisant un carré de Polybe. Le message est intercepté par des élèves mais personne ne dispose de la clef pour le décoder :
    34122413111425144515221514341451252211351251215121221122131445111421321423451431143414213212111413
    Sachant que le mot exercice a de forte chance d’être utilisé dans le message, décoder ce message.

C) La scytale

Une technique de chiffrement également ancienne consiste à changer l’ordre des lettres d’un texte, à les mélanger en quelque sorte. Quand il est question de codes secrets, on parle alors de chiffrement par transposition.

On écrit sur un ruban enroulé autour d’un bâton, appelé scytale. Une fois déroulé, le message devient incompréhensible.

Voici le message à coder :
LE COLLEGE WILLY RONIS SE SITUE DANS L’ACADEMIE DE CRETEIL
Le chiffrement par scytale peut être simulé en utilisant un rectangle.

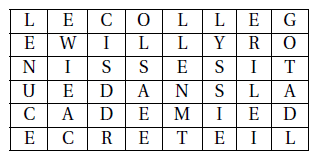
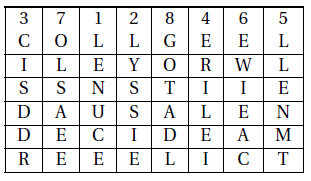
On se donne ensuite une permutation des nombres de 1 à 8 (si le rectangle a 8 colonnes). Par exemple : 37128465. La première colonne est alors recopiée en troisième position, la deuxième en septième position…

Cependant, il est difficile de mémoriser une suite de chiffres comme 37128465. Il est plus simple de se souvenir d’un mot ayant un sens comme FRACTION. Pour le trouver, on classe les lettres de FRACTION dans l’ordre alphabétique : ACFINORT. Dans FRACTION, chaque lettre est alors remplacée par son ordre d’apparition dans ACFINORT, en excluant les doublons. Ainsi, la clef FRACTION cache la permutation 37128465.

  1. Deux élèves du collège souhaitent utiliser un chiffrement par scytale pour communiquer. La clef de chiffrement est CRAYON. Aidez les à coder le message suivant :
    RENDEZ VOUS APRES LES COURS CHEZ ALEXANDRE
  2. Déchiffrer le message suivant en utilisant la clé de chiffrement TRIANGLE.
    NEBREAENORMDJMLOANUEDTUPLPALOTTRSAENBESDMIOMEAQLICRUOHEIAOPELMIU

Vous pourriez aimer:

  1. Chapitre 1 : multiplication et division de nombres relatifs
  2. Chapitre 9 : Angles et parallélisme
  3. Sujet et correction brevet blanc mathématiques de mai 2023

Laisser un commentaire