Chapitre 22
Probabilités
Chapitre 22 : Probabilités
A) Expérience aléatoire
Définition : Une expérience est dite aléatoire lorsqu’on ne peut pas prévoir avec certitude le résultat (ou issue).
Définition : Un événement est constitué par certaines issues d’une expérience aléatoire.
Exemples : Dans chacune des situations ci-dessous, plusieurs issues (ou résultats) sont possibles.
- Lancer une pièce équilibrée est une expérience aléatoire. Cette expérience a deux issues : pile ou face.
- Tirer une boule dans une urne est une expérience aléatoire. Cette expérience a deux issues : rouge ou jaune.
- Dans le troisième exemple, on peut s’intéresser à l’événement « obtenir un nombre impair ». On a $6$ chances sur $8$ d’obtenir un nombre impair.
B) Notion de probabilité
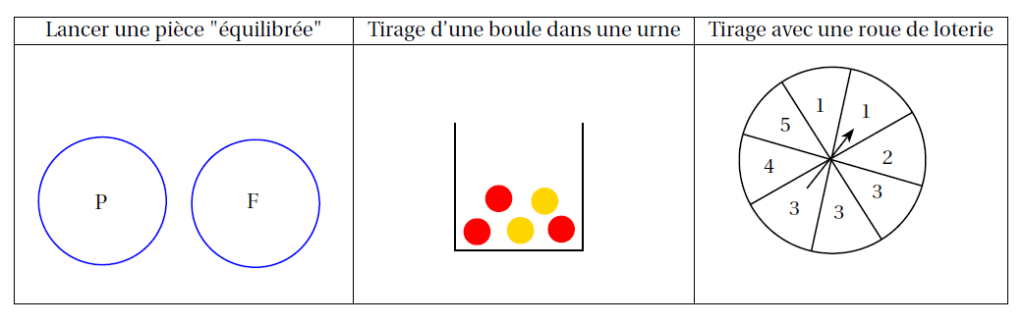
Exemples : Retour à l’exemple précédent :
- Dans le premier exemple, on a $1$ chance sur $2$ de tirer « Pile ». On dira alors que la probabilité de cette issue est égale à $\dfrac{1}{2}$.
- Dans le deuxième exemple, la probabilité de tirer une boule rouge est de $\dfrac{3}{5}$. Il y a $60$ % de chance d’obtenir une boule rouge.
- Dans le troisième exemple, la probabilité de tomber sur une case comportant le chiffre $1$ est $\dfrac{2}{8}$
Définition : La probabilité d’une issue est égale au quotient de nombre d’issues favorables (issues dans lesquelles on obtient le résultat) par le nombre total d’issues possibles.
On peut ainsi positionner un événement sur une échelle de probabilité graduée de 0 à 1 :
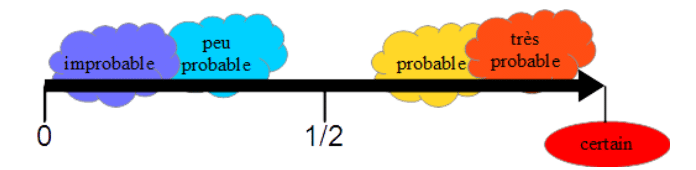
Propriétés :
- La probabilité d’une issue est un nombre compris entre $0$ et $1$.
- La somme des probabilités des issues d’une expérience aléatoire est égale à $1$.
Exemple : En reprenant l’exemple de la roue de loterie des exemples précédents :
$\dfrac{2}{8}+\dfrac{1}{8}+\dfrac{3}{8}+\dfrac{1}{8}+\dfrac{1}{8}=\dfrac{2+1+3+1+1}{8}=\dfrac{8}{8}=1$
Remarques :
- Une probabilité peut s’exprimer sous diverses formes (décimale, fractionnaire, pourcentage).
- En classe de 6e, on étudie des expériences aléatoires où toutes les issues ont la même probabilité. On appelle ces expériences des situations d’équiprobabilité.
C) Expérimentation du hasard
Exemple : Une expérience aléatoire consiste à lancer deux fois une pièce de monnaie équilibrée et à noter le résultat obtenu : deux fois Face, Pile puis Face, Face puis Pile, deux fois Pile.
On peut représenter la situation à l’aide d’un arbre ou d’un tableau :
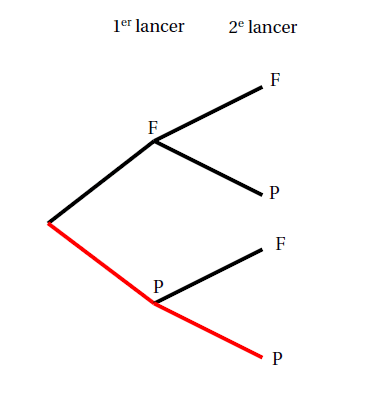
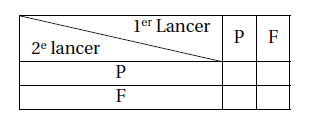
On réalise 500 fois cette simulation avec le logiciel Scratch. On observe que la proportion d’apparition de deux fois Pile est 0,247, celle proportion est proche de la probabilité égale à 0,25 d’obtenir deux fois Pile lors du lancer des deux pièces.