Chapitre 11
La division euclidienne
Chapitre 11 : La division euclidienne
A) Définition
Définition : Effectuer la division euclidienne d’un nombre entier, appelé le dividende, par un nombre entier différent de $0$, appelé le diviseur, revient à trouver deux nombres entiers, appelés le quotient et le reste, vérifiant :
\[\text{Dividende}=\text{Diviseur}\times \text{Quotient}+\text{Reste}~~~~~~\text{avec Reste < Diviseur}\]
Exemple :
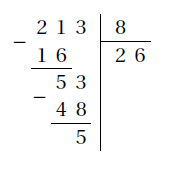
\[213=8\times 26+5\]
- $213$ est le dividende.
- $8$ est le diviseur.
- $26$ est le quotient.
- $5$ est le reste.
B) Critères de divisibilité
Définition : Le nombre a est divisible par le nombre $b$ ($b\neq 0$) si le reste de la division euclidienne de $a$ par $b$ est $0$. On a donc $a = b\times q$.
• $b$ et $q$ sont des diviseurs de $a$.
• $a$ est un multiple de $b$.
Exemple : $65=13\times 5$. On peut alors dire:
- $65$ est un multiple de $13$.
- $65$ est divisible par $13$.
- $13$ est un diviseur de $65$.
Propriétés :
- Un nombre entier est divisible par $2$ lorsque son chiffre des unités est $0$ ; $2$ ; $4$ ; $6$ ; $8$.
- Un nombre entier est divisible par $5$ lorsque son chiffre des unités est $0$ ou $5$.
- Un nombre entier est divisible par $10$ lorsque son chiffre des unités est $0$.
- Un nombre entier est divisible par $3$ lorsque la somme de ses chiffres est un multiple de $3$.
- Un nombre entier est divisible par $9$ lorsque la somme de ses chiffres est un multiple de $9$.
Exemples :
- $532$ est divisible par $2$ car son chiffre des unités est $2$.
- $5~430$ est divisible par $2$, par $5$ et par $10$ car son chiffre des unités est $0$.
Vocabulaire :
- Les nombres entiers divisibles par $2$ sont appelés les nombres pairs.
- Les nombres entiers non divisibles par $2$ sont appelés les nombres impairs.
Exemple : $6~450$ est divisible par $3$ mais pas par $9$. En effet $6+4+5+0 = 15$ et $15$ est un multiple de $3$ mais pas de $9$.
C) Résoudre des problèmes
Exemple : Pour une course d’orientation, les $245$ élèves de l’école et leurs $38$ accompagnateurs doivent être transportés par car. Un car peut transporter $46$ passagers.
Combien de cars la directrice doit-elle réserver pour pouvoir transporter tous les élèves et tous les accompagnateurs ?
Je calcule le nombre total de passagers à transporter :
\[245+38=283\]
Il y a donc $283$ passagers à transporter.
Je calcule ensuite le nombre de cars à prévoir.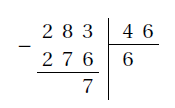
$6$ cars ne suffiront pas car il restera encore $7$ passagers à transporter. La directrice doit donc réserver $6+1=7$ cars.
Bilan : Dans ce chapitre, je dois :
- Savoir poser et effectuer une division euclidienne.
- Comprendre la relation entre dividende, diviseur, quotient et reste.
- Connaître les critères de divisibilité par $2$, par $3$, par $5$, par $9$ et par $10$.
- Résoudre des problèmes mobilisant la division euclidienne.