
Propriété : Dans un triangle, la somme des mesures des trois angles est égale à $180\text{°}$.
Démonstration :
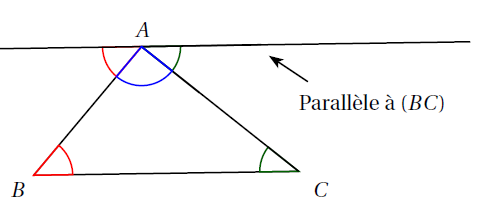
On trace la parallèle à la droite $(BC)$ passant par $A$.
Les angles rouges sont alternes-internes ainsi que les angles verts. Or, d’après la propriété précédente, si deux droites parallèles sont coupées par une sécante, alors les angles alternes-internes qu’elles forment ont la même mesure.
Ainsi, les angles rouges ont la même mesure et les angles verts ont la même mesure.
On en déduit que dans le triangle $ABC$ :
\[\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180\text{°}\]
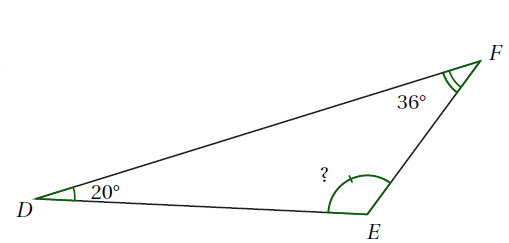
Exemple : Calculer la mesure de l’angle $\widehat{DEF}$.
Dans un triangle, la somme des mesures des angles égales $180\text{°}$. Ainsi :
$\widehat{DEF}+\widehat{DFE}+\widehat{FDE}=180\text{°}$
$\widehat{DEF}+36\text{°}+20\text{°}=180\text{°}$
$\widehat{DEF}=180\text{°}-(20\text{°}+36\text{°})$
$\widehat{DEF}=180\text{°}-56\text{°}$
$\widehat{DEF}=124\text{°}$
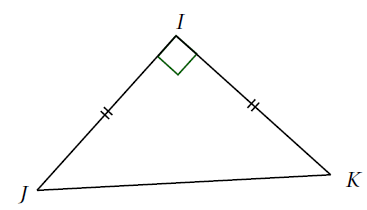
Exemple : Le triangle $IJK$ est rectangle isocèle en $I$. Calculer la mesure de l’angle $\widehat{IKJ}$.
$IKJ$ est isocèle en $I$ donc ses angles à la base ont la même mesure.
Ainsi, $\widehat{IKJ}=\widehat{IJK}$.
Ainsi :
$\widehat{IKJ}=\dfrac{180\text{°}-90\text{°}}{2}=45\text{°}$
Propriété : Si un triangle est équilatéral alors chacun de ses angles mesure $60\text{°}$.
Exemple :
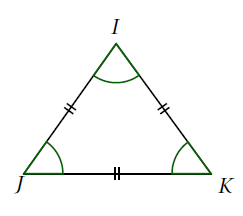
Le triangle $IJK$ est équilatéral donc ses 3 angles ont la même mesure.
$\widehat{IJK}=\widehat{IKJ}=\widehat{JIK}$.
Donc $3\times \widehat{IJK}=180\text{°}$.
Ainsi $\widehat{IJK}=\widehat{IKJ}=\widehat{JIK}=60\text{°}$.
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |