Chapitre 6
Comparer et effectuer des opérations avec des fractions
Chapitre 6 : Comparer et effectuer des opérations avec des fractions
A) Comparer des fractions à 1 ou à 1/2
Propriétés :
- Si le numérateur est inférieur au dénominateur alors la fraction est inférieure à 1.
- Si le numérateur est supérieur au dénominateur alors la fraction est supérieure à 1.
- Si le numérateur est égal au dénominateur alors la fraction est égale à 1.
Propriétés :
- Si le double du numérateur est inférieur au dénominateur alors la fraction est inférieure à $\dfrac{1}{2}$.
- Si le double du numérateur est supérieur au dénominateur alors la fraction est supérieure à $\dfrac{1}{2}$.
Exemples :
- $\dfrac{17}{15}>1$ et $\dfrac{14}{15}<1$ donc $\dfrac{17}{15}>\dfrac{14}{15}$.
- $\dfrac{6}{15}<\dfrac{1}{2}$ et $\dfrac{11}{13}>\dfrac{1}{2}$ donc $\dfrac{6}{15}<\dfrac{11}{13}$.
- $\dfrac{8}{8}=1$ car le numérateur est égal au dénominateur.
B) Comparer des fractions de même dénominateur ou de même numérateur
Propriété : Si deux fractions ont le même dénominateur, la plus grande est celle qui a le plus grand numérateur.
Exemple : Trois parts d’un gâteau coupé en 4, c’est davantage qu’une part de ce même gâteau.
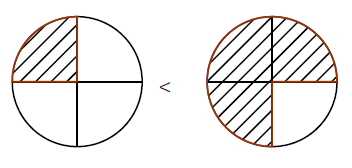
$\dfrac{1}{4}<\dfrac{3}{4}$
Propriété : Si deux fractions ont le même numérateur, la plus grande est celle qui a le plus petit dénominateur.
Exemple : On a une plus grande part de gâteau quand il est coupé en 4 que quand il est coupé en 8.
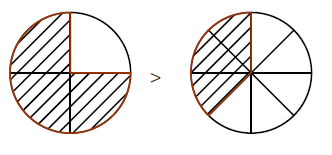
$\dfrac{3}{4}>\dfrac{3}{8}$
Exemple : Comparer $\dfrac{13}{6}$ et $\dfrac{43}{12}$.
$\dfrac{13}{6}=\dfrac{13\times \textcolor{red}{2}}{6\times \textcolor{red}{2}}=\dfrac{26}{12}$
Or $26<43$, donc : $\dfrac{26}{12}<\dfrac{43}{12}$
Ainsi : $\dfrac{13}{6}<\dfrac{43}{12}$
C) Additionner et soustraire des fractions
Règle : Pour additionner (ou pour soustraire) deux quotients de même dénominateur, on additionne (ou on soustrait)
les numérateurs et on conserve le dénominateur commun.
Exemples :
- $\dfrac{13}{\textcolor{red}{4}}+\dfrac{6}{\textcolor{red}{4}}=\dfrac{13+6}{\textcolor{red}{4}}=\dfrac{19}{\textcolor{red}{4}}$
- $\dfrac{18}{\textcolor{red}{12}}-\dfrac{11}{\textcolor{red}{12}}=\dfrac{18-11}{\textcolor{red}{12}}=\dfrac{7}{\textcolor{red}{12}}$
Règle : Pour additionner (ou pour soustraire) deux fractions de dénominateurs différents, on les écrit avec le même
dénominateur.
Exemples :
- $\dfrac{1}{2}+\dfrac{3}{4}=\dfrac{1\textcolor{red}{\times 2}}{2\textcolor{red}{\times 2}}+\dfrac{3}{4}=\dfrac{2}{4}+\dfrac{3}{4}=\dfrac{5}{4}$
- $\dfrac{7}{5}-\dfrac{1}{3}=\dfrac{7\textcolor{red}{\times 3}}{5\textcolor{red}{\times 3}}-\dfrac{1\textcolor{red}{\times 5}}{3\textcolor{red}{\times 5}}=\dfrac{21}{15}-\dfrac{5}{15}=\dfrac{16}{15}$
- $3+\dfrac{5}{4}=\dfrac{12}{4}+\dfrac{5}{4}=\dfrac{17}{4}$
D) Prendre une fraction d'un nombre
Propriété : Pour calculer une fraction d’un nombre entier, on multiplie la fraction par le nombre.
Exemple : Pour calculer $\dfrac{5}{3}$ de $6$, on calcule $\dfrac{5}{3}\times 6$.
1ère Méthode : on calcule 5 fois le tiers de 6 :
\[\dfrac{5}{3}\times 6=5\times (6\div 3)=5\times 2=10\]
2ème Méthode : on voit $\dfrac{5}{3}\times 6$ comme $\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}$ :
\[\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{3}=\dfrac{5+5+5+5+5+5}{3}=\dfrac{5\times 6}{3}=\dfrac{30}{3}=10\]