Chapitre 6
La proportionnalité
Chapitre 6 : La proportionnalité
A) Calculer une quatrième proportionnelle
Vocabulaire : Dans un tableau de proportionnalité, lorsqu’on connaît trois nombres non nuls, on peut calculer le quatrième nombre manquant. Ce nombre manquant est appelé une quatrième proportionnelle.
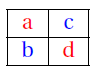On peut alors écrire l’égalité des produits en croix :
\[\textcolor{red}{a}\times \textcolor{red}{d}=\textcolor{blue}{b}\times \textcolor{blue}{c}\] Démonstration : Ce tableau est un tableau de proportionnalité donc les quotients $\dfrac{a}{b}$ et $\dfrac{c}{d}$ sont égaux.
Ainsi,
\[\dfrac{a}{b}=\dfrac{c}{d}\]Donc :
\[\dfrac{a\times d}{b\times d}=\dfrac{c\times b}{d\times b}\]Ces deux fractions ont des dénominateurs égaux, donc leurs numérateurs sont également égaux :
\[a\times d=b\times c\]
Exemples : $4$ kg de cerises coûtent $11,20$ euros. Combien coûtent $5$ kg de cerises ?
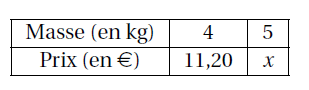
\begin{eqnarray*}
4\times x&=&5\times 11,20\\
x&=&\dfrac{5\times 11,20}{4}\\
x&=&14
\end{eqnarray*}
$5$ kg de cerises coûtent $14$ euros.
B) Reconnaître un graphique représentant une situation de proportionnalité
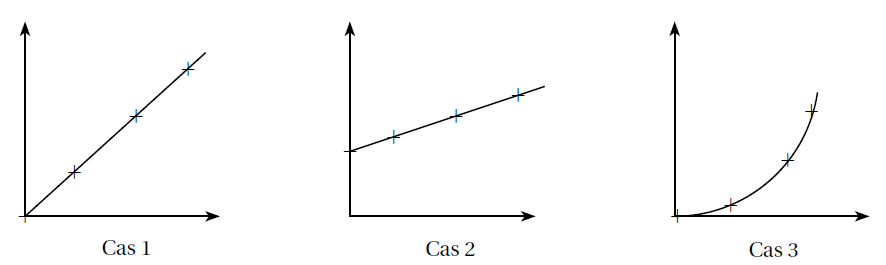
Propriété (admise) : Une situation représentée par des points alignés avec l’origine du repère est équivalente à une situation de proportionnalité.
Exemples : Le(s)quel(s) de ces trois graphiques représentent une situation de proportionnalité ?
- Cas 1 : Les points sont alignés avec l’origine du repère donc c’est une situation de proportionnalité.
- Cas 2 : Les points sont alignés mais pas avec l’origine du repère donc ce n’est pas une situation de proportionnalité.
- Cas 3 : Les points ne sont pas alignés donc ce n’est pas une situation de proportionnalité.
C) Appliquer ou calculer un pourcentage
Propriété : $p$ désigne un nombre. Calculer $p\%$ d’une quantité c’est multiplier cette quantité par $\dfrac{p}{100}$.
Exemple : Calculer $30 \%$ de $50~\text{L}$.
\[\dfrac{30}{100}\times 50~\text{L}=0,30\times 50~\text{L}=15~\text{L}\]
$30 \%$ de $50~\text{L}$ c’est donc $15~\text{L}$.
Méthode : Calculer un pourcentage revient à écrire une proportion de dénominateur 100.
D) Agrandissement-réduction
Définition : Agrandir ou réduire une figure, c’est construire une figure de même forme en multipliant les longueurs de la figure initiale par un nombre $k$ strictement positif.
Vocabulaire : On dit que $k$ est le rapport (ou coefficient) d’agrandissement ou de réduction.
- Si $k>1$, il s’agit d’un agrandissement.
- Si $0<k<1$, il s’agit d’une réduction.
Propriétés : Dans un agrandissement ou une réduction, de rapport $k$ :
- les longueurs sont toutes multipliées par $k$ ;
- les mesures des angles sont conservées.
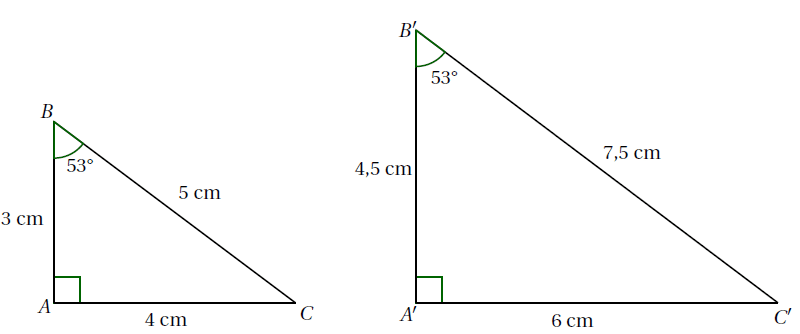
Exemple : Sur la figure ci-dessous, le triangle $A’B’C’$ est un agrandissement du triangle $ABC$. Les longueurs ont été multipliées par $1,5$.
En effet :
\[3~\text{cm}\textcolor{red}{\times 1,5}=4,5~\text{cm}~~~~4~\text{cm}\textcolor{red}{\times 1,5}=6~\text{cm}~~~~5~\text{cm}\textcolor{red}{\times 1,5}=7,5~\text{cm}\]
La mesure des angles est en revanche conservée.
Propriétés : Dans un agrandissement ou une réduction de rapport $k$ :
- l’aire d’une surface est multipliée par $k^{2}$ ;
- le volume d’un solide est multiplié par $k^{3}$.
Exemple : Sur la figure ci-dessous, le 2ème pavé droit est un agrandissement du 1er pavé droit de coefficient $2$.
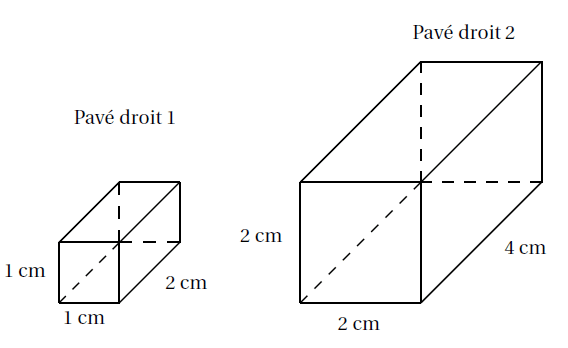
Or :
\[V_{\text{pavé droit 1}}=1~\text{cm}\times 1~\text{cm}\times 2~\text{cm}=2~\text{cm}^{3}\]\[V_{\text{pavé droit 2}}=2~\text{cm}\times 2~\text{cm}\times 4~\text{cm}=16~\text{cm}^{3}\]
Le volume a été multiplié par $2^{3}=8$.