Section d'excellence
Suite de Farey et cercles de Ford

A) Introduction
Extrait du document les fractions de Monsieur Farey, Robert FERACHOGLOU, Lycée Le Castel à Dijon :
Le géologue anglais John Farey suggéra en 1816 de ranger dans l’ordre croissant les fractions irréductibles, comprises entre 0 et 1, et dont le dénominateur ne dépasse pas une valeur donnée.
Par exemple, celles dont le dénominateur est inférieur ou égal à 3 se rangent ainsi :
\[\dfrac{0}{1},\dfrac{1}{3},\dfrac{1}{2},\dfrac{2}{3},\dfrac{1}{1}\]
Farey remarqua qu’une telle suite possédait de jolies propriétés. Cependant Farey, qui n’était qu’un mathématicien moyen (et même un géologue quelconque, puisqu’il est aujourd’hui presque entièrement oublié en tant que tel), ne donna aucune preuve des résultats publiés. C’est Louis Augustin Cauchy qui démontra les propriétés en question ; ce dernier, bon prince, a conservé le nom de Farey attaché à ces suites de fractions.
Ce document propose de mettre en évidence quelques propriétés des suites de Farey et des cercles de Ford.
B) Définitions et premières conjectures
Définition : La suite de Farey de rang $n$, noté $F_{n}$ , est la suite finie formée par les fractions irréductibles de dénominateur inférieur ou égal à $n$ comprises entre 0 et 1, rangées dans l’ordre croissant.
Exemples :
- $F_{1}=\left(\dfrac{0}{1},\dfrac{1}{1}\right)$
- $F_{2}=\left(\dfrac{0}{1},\dfrac{1}{2},\dfrac{1}{1}\right)$
- $F_{3}=\left(\dfrac{0}{1},\dfrac{1}{3},\dfrac{1}{2},\dfrac{2}{3},\dfrac{1}{1}\right)$
Définition : Soient deux fractions consécutifs $\dfrac{a}{b}$ et $\dfrac{c}{d}$ d’une suite de Farey.
On appelle fraction médiane des fractions $\dfrac{a}{b}$ et $\dfrac{c}{d}$ la fraction $\dfrac{p}{q}$ telle que :
\[\dfrac{p}{q}=\dfrac{a+c}{b+d}\]
Dans un premier, les élèves de la section ont déterminé $F_{4}$, $F_{5}$ et $F_{6}$ :
- $F_{4}=\left(\dfrac{0}{1},\dfrac{1}{4},\dfrac{1}{3},\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},\dfrac{1}{1}\right)$
- $F_{5}=\left(\dfrac{0}{1},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{1}{2},\dfrac{3}{5},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5},\dfrac{1}{1}\right)$
- $F_{6}=\left(\dfrac{0}{1},\dfrac{1}{6},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{1}{2},\dfrac{3}{5},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5},\dfrac{5}{6},\dfrac{1}{1}\right)$
-
- La fraction $\dfrac{1}{2}$ occupe la position médiane dans $F_{n}$.
- En choisissant deux fractions consécutives de $F_{n}$ (notées $\dfrac{a}{b}<\dfrac{c}{d}$) et en calculant $bc-ad$, on obtient toujours $1$ : \[bc-ad=1\]
- Si $\dfrac{a}{b}$, $\dfrac{e}{f}$ et $\dfrac{c}{d}$ sont, dans cet ordre, trois fractions successives d’une même suite de Farey, alors (addition des cancres) :\[\dfrac{e}{f}=\dfrac{a+c}{b+d}\]
- $F_n$ est la réunion de $F_{n-1}$ et de l’ensemble des fractions médianes de $F_{n-1}$ de dénominateur égal à $n$.
Remarques :
- La première conjecture n’a pas été démontrée en classe.
- La deuxième conjecture n’a également pas été démontrée en classe mais vérifiée dans certains cas :
Dans $F_{5}$, on choisit $\dfrac{a}{b}=\dfrac{2}{5}$ et $\dfrac{c}{d}=\dfrac{1}{2}$. On obtient alors :
\[bc-ad=5\times 1-2\times 2=5-4=1\] - La troisième conjecture peut-être démontrée en classe avec les très bons élèves :
Démonstration : Soient 3 termes consécutifs d’une suite de Farey : $\dfrac{a}{b}<\dfrac{p}{q}<\dfrac{c}{d}$.
On a donc :
\[
\left \{
\begin{array}{c @{=} c}
pb-aq = 1 \\
cq-pd = 1
\end{array}
\right.
\]On multiplie la première équation par $c$ et la deuxième par $a$ :
\[
\left \{
\begin{array}{c @{=} c}
pb-aq =1~~~~\times c \\
cq-pd =1~~~~\times a
\end{array}
\right.
\]On multiplie la première équation par $d$ et la deuxième par $b$ :
\[
\left \{
\begin{array}{c @{=} c}
pb-aq = 1~~~~\times d \\
cq-pd = 1~~~~\times b
\end{array}
\right.
\]On obtient alors :
\[
\left \{
\begin{array}{c @{=} c}
pbc-aqc = c \\
cqa-pda = a
\end{array}
\right.
\]\[
\left \{
\begin{array}{c @{=} c}
pbd-aqd = d\\
cqb-pdb = b
\end{array}
\right.
\]Par somme :
\[pbc-pad=a+c\]\[
cqb-adq=b+d
\]On en déduit en factorisant les membres de gauche :
\[
\left \{
\begin{array}{c @{=} c}
p(bc-ad) = a+c\\
q(bc-ad) = b+d
\end{array}
\right.
\]Par quotient :
\[\dfrac{p(bc-ad)}{q(bc-ad)}=\dfrac{a+c}{b+d}\]Ainsi, en simplifiant par $(bc-ad)$ :
\[\dfrac{p}{q}=\dfrac{a+c}{b+d}\] - Les fractions de $F_7$ sont ainsi obtenues en ajoutant aux fractions de $F_6$ l’ensemble des fractions médianes de $F_6$ de dénominateur égal à 6. Par ailleurs, les fractions médianes de $F_6$ sont les premières à apparaître entre deux fractions de $F_7$. Ainsi :
$F_{7}=\left(\dfrac{0}{1},\dfrac{1}{7},\dfrac{1}{6},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{3}{7},\dfrac{1}{2},\dfrac{4}{7},\dfrac{3}{5},\dfrac{2}{3},\dfrac{5}{7},\dfrac{3}{4},\dfrac{4}{5},\dfrac{5}{6},\dfrac{6}{7},\dfrac{1}{1}\right)$
C) Lien avec les cercles de Ford
Définition : Soient $a$ et $b$ deux entiers non nuls. On représente sur l’axe des abscisses et au dessus de chaque fraction $\dfrac{a}{b}$
le cercle de rayon $\dfrac{1}{2b^{2}}$ , appelé cercle de Ford de $\dfrac{a}{b}$.
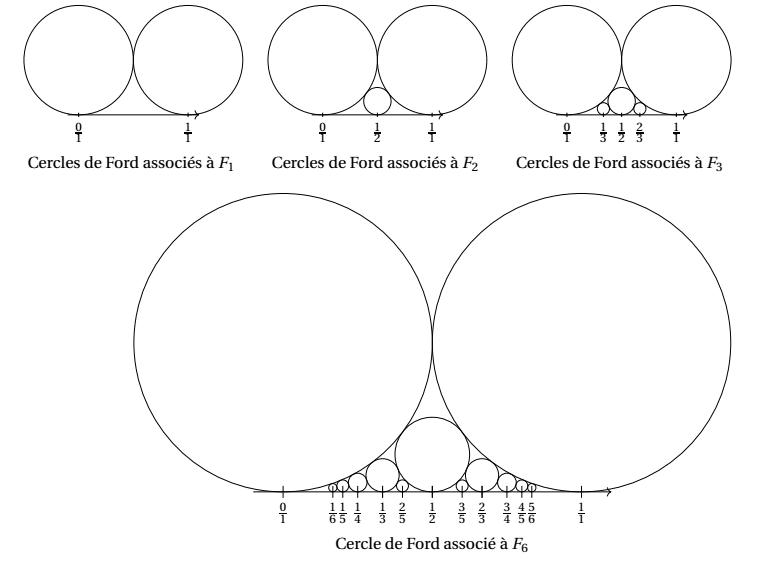
Les élèves ont conjecturé que les cercles de Ford associés à deux termes consécutifs d’une même suite de Farey sont tangents entre eux.
Démonstration : Voici la preuve pour les cercles de Ford associés aux fractions $\dfrac{1}{3}$ et $\dfrac{1}{2}$ :
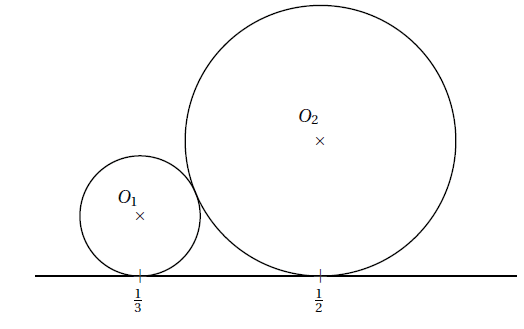
On a :
- $0_{1}A=\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3}{6}-\dfrac{2}{6}=\dfrac{1}{6}$
- $0_{2}A=\dfrac{1}{2\times 2^{2}}-\dfrac{1}{2\times 3^{2}}=\dfrac{1}{8}-\dfrac{1}{18}=\dfrac{9}{72}-\dfrac{4}{72}=\dfrac{5}{72}$
Le triangle $O_{1}O_{2}A$ est rectangle en $A$.
D’après le théorème de Pythagore :
\begin{eqnarray*}
O_{1}O_{2}^{2}&=&0_{1}A^{2}+0_{2}A^{2}\\
O_{1}O_{2}^{2}&=&\left(\dfrac{1}{6}\right)^{2}+\left(\dfrac{5}{72}\right)^{2}\\
O_{1}O_{2}^{2}&=&\dfrac{1}{36}+\dfrac{25}{5~184}\\
O_{1}O_{2}^{2}&=&\dfrac{144}{5~184}+\dfrac{25}{5~184}\\
O_{1}O_{2}^{2}&=&\dfrac{169}{5~184}\\
O_{1}O_{2}&=&\sqrt{\dfrac{169}{5~184}}\\
O_{1}O_{2}&=&\dfrac{13}{72}
\end{eqnarray*}
Or : $O_{1}I+IO_{2}=\dfrac{1}{8}+\dfrac{1}{18}=\dfrac{9}{72}+\dfrac{4}{72}=\dfrac{13}{72}$
Donc :
\[O_{1}O_{2}=O_{1}I+IO_{2}\]Ceci prouve que les deux cercles sont tangents.
Les propriétés précédentes des cercles de Ford ont inspiré certains artistes. Voici une image de Jos Leys, artiste géomètre :
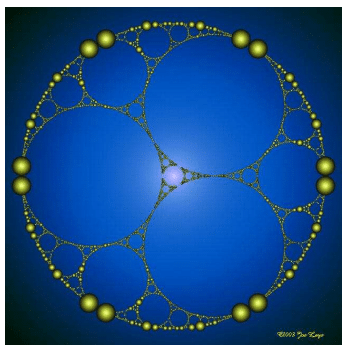
D’autres images sur le site de Jos Leys.
D) Approximation d'un réel
Voici un programme Scratch donnant un encadrement de $\dfrac{1}{\sqrt{n}}$ par des fractions dont le dénominateur ne dépasse pas $20$ :