A) Polyèdres convexes
Définition : Un polyèdre est un solide dont toutes les faces sont des polygones.
Définition : Un polyèdre est convexe si toutes ses diagonales sont entièrement contenues dans son intérieur.
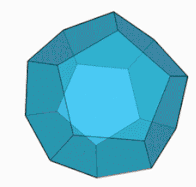
Exemple : Un polyèdre convexe (Dodécaèdre régulier).
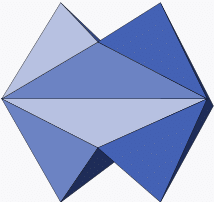
Un polyèdre non convexe (Icosaèdre de Jessen).
B) Caractéristique d'Euler d'un polyèdre convexe
Les élèves se sont alors intéressés à la caractéristique d’Euler d’un polyèdre convexe.
Définition : La caractéristique d’Euler est la quantité $s-a+f$ où $s$ est le nombre de sommets, $a$ le nombre d’arêtes et $f$ le nombre de faces.
Pour les aider à établir une conjecture, ils disposaient de polyèdres convexes posés sur un îlot de la salle mais également de GéoGébra.
Exemples :
Cube adouci
Dodécaèdre rhombique
Les élèves finissent par conjecturer que la caractéristique d’Euler pour les polyèdres convexes est toujours égale à 2.
Théorème de Descartes-Euler : La quantité $s-a+f$ vaut 2 pour un polyèdre convexe.
Le théorème est formulé par Leonhard Euler en 1752. Il semble cependant que Descartes ait prouvé une relation
analogue dans un traité jamais publié. C’est la raison pour laquelle cette relation porte ce double nom.
Remarque : ce théorème est vrai uniquement pour les polyèdres convexes de genre 0.
C) Démonstration de la conjecture
Pour démontrer cette conjecture, il a fallu déformer le polyèdre, en l’aplatissant et en écartant
vers l’extérieur les côtés de cette face manquante. Nous obtenons alors le graphe planaire du polyèdre. En considérant
que tout l’extérieur du graphe obtenu représente la face enlevée au polyèdre de départ, le nombre de sommets,
d’arêtes et de faces n’a pas changé. Il suffit donc de démontrer que la caractéristique d’Euler d’un graphe planaire est
toujours égale à 2.
Exemple : graphe planaire d’un cube.
Exemple : graphes planaires de certains polyèdres.
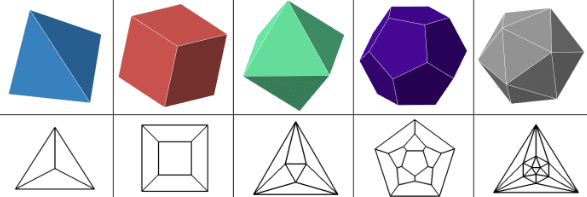
Définition : Un graphe planaire est obtenu de la façon suivante : on choisit des points du plan appelés sommets. On peut ensuite choisir de relier les points distincts par des segments appelés arêtes, telles qu’elles ne s’intersectent pas.
Définition : On appelle face du graphe une région du plan entourée par des segments.
Remarque : Lors du dénombrement des faces, il ne faut pas oublier la face extérieure (celle qui est infinie).
Exemple : Un graphe planaire.
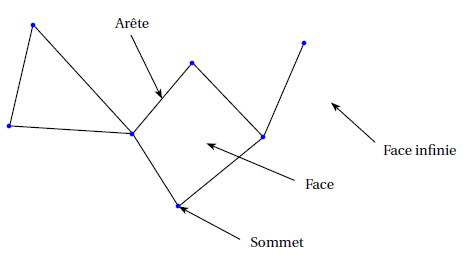
Ce graphe possède 7 sommets, 8 arêtes et 3 faces (2 faces + la face infinie).
Sa caractéristique d’Euler, noté $\chi$ vaut alors :
\[\chi =7-8+3=-1+3=2\]
Les élèves ont d’abord remarqué que transformer un graphe en figure ne comportant que des triangles et sans changer sa caractéristique d’Euler est toujours possible :
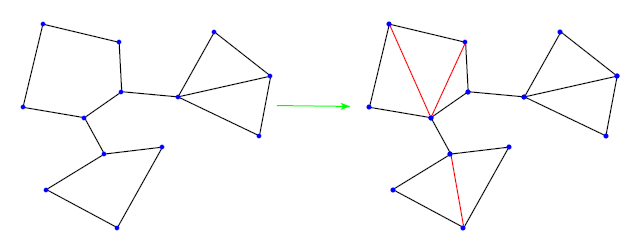
Ils ont ensuite établi quelques règles de simplification (qu’ils ont démontré sur des exemples) qui ne changent pas la caractéristique d’Euler d’un graphe :
- on peut supprimer certaines arêtes du graphe sans changer son $\chi $.
- on peut supprimer un chapeau du graphe sans changer son $\chi $.
Démonstration (sur un exemple) : supprimer un chapeau ne change pas la caractéristique d’un graphe.
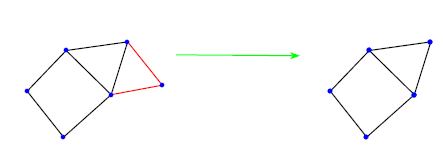On remarque sur l’exemple ci-dessus que retirer $n$ chapeaux reviendrait à retirer $n$ sommets, $n$ faces et $2n$ arêtes. Ainsi, en appelant $\chi’$ la caractéristique d’Euler du graphe d’arrivée :
\[\chi’ =(s-n)-(a-2n)+f-n=s-n-a+2n+f-n=s-a+f=\chi\]
En appliquant les règles précédentes, on peut toujours transformer un graphe planaire quelconque en un segment dont la caractéristique d’Euler vaut 2. Ainsi, la caractéristique d’Euler d’un graphe planaire est toujours égale à 2 et il en est de même pour un polyèdre convexe.
