Chapitre 23
Les volumes
Chapitre 23 : Les volumes
A) Volume d'un solide
Définition : Le volume d’un solide est l’espace occupé par ce solide dans une unité de volume donnée.
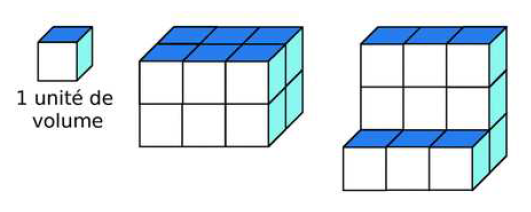
Exemple : Pour trouver le volume de chaque solide, il suffit de compter le nombre d’unités de volume qui le constituent. Les deux solides ci-dessous ont pour volume $12$ (en unités de volume) alors qu’ils n’ont pas la même forme.
B) Unités de volume et de capacité
Définition : Une unité de volume souvent utilisée est le $\text{m}^{3}$. Un mètre cube est le volume occupé par un cube d’arête $1$ mètre.
Exemple : On remarque que l’on peut placer $1~000$ cubes de côté $1~\text{cm}$ dans un cube de côté $1~\text{dm}$ :
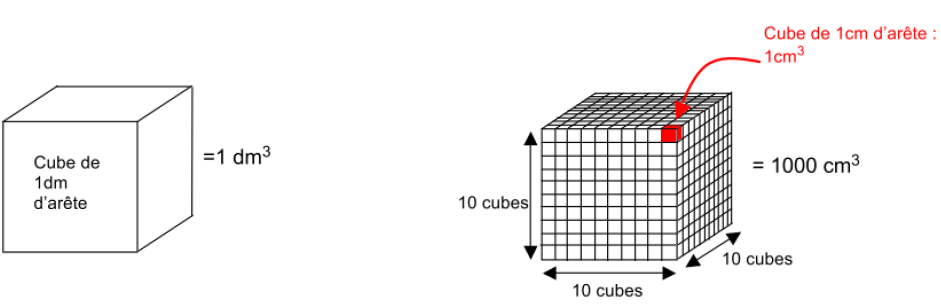
$1~\text{dm}^{3}=1~000~\text{cm}^{3}$
Définition : Pour mesurer des capacités, on utilise des unités de volume spécifiques. L’unité de capacité de base est le litre (L) qui est la quantité de liquide que peut contenir un cube d’un décimètre de côté. Ainsi :
$1~\text{L}=1~\text{dm}^{3}$
Exemple : On peut vider une bouteille de lait de $1~\text{L}$ dans un cube de côté $1~\text{dm}$. Le liquide arrivera à ras bord :
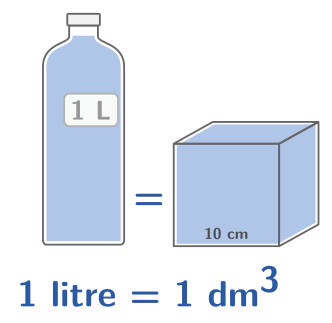
Tableau des unités de volume et de capacité :
Exemples :
- $125~\text{cm}^{3}=125\div 1~000~000~\text{m}^{3}=0,000125~~\text{m}^{3}$
- $12~\text{m}^{3}=12\times 1~000~\text{dm}^{3}=12~000~\text{dm}^3=12~000~L$
- $7,3~\text{dm}^{3}=7,3\times 1~000~\text{cm}^{3}=7 300~\text{cm}^{3}$
C) Volume d'un parallélépipède rectangle
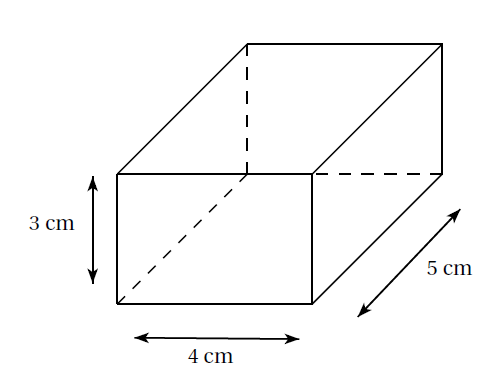
Exemple : Le volume du parallélépipède rectangle ci-dessous est :
$V=5~\text{cm}\times 4~\text{cm}\times 3~\text{cm}=60~\text{cm}^{3}$
