
Définition : Une équation est une égalité dans laquelle figurent un ou plusieurs nombres inconnus, désignés le plus souvent par des lettres.
Définition : Une équation est dite du premier degré à une inconnue $x$ lorsqu’elle peut s’écrire sous la forme $ax+b=cx+d$ (où $a,b,c$ et $d$ désignent des nombres avec $a\neq c$).
Exemple : $2,1x-0,4=1,3x+0,1$ est une équation du premier degré à une inconnue $x$.
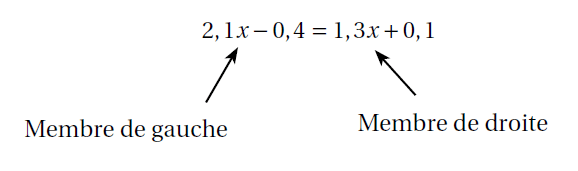
Définition : Une solution d’une équation est une valeur de l’inconnue pour laquelle l’égalité est vrai.
Exemple : Les nombres $1$ et $-2$ sont-ils solutions de l’équation suivante :
\[3x+2=9x-4\]
On calcule le membre de gauche : $3\times \textcolor{red}{1}+2=5$.
On calcule le membre de droite : $9\times \textcolor{red}{1}-4=5$.
Les résultats étant identiques on conclut que $1$ est solution de cette équation.
On calcule le membre de gauche : $3\times (\textcolor{red}{-2})+2=-6+2=-4$.
On calcule le membre de droite : $9\times (\textcolor{red}{-2})-4=-18-4=-22$.
Les résultats étant différents on conclut que $-2$ n’est pas solution de cette équation.
Définition : Résoudre une équation c’est trouver toutes ses solutions.
Propriété : On obtient une nouvelle équation qui a les mêmes solutions que l’équation initiale lorsqu’on ajoute ou on soustrait un même nombre aux deux membres de cette équation.
Démonstration : Si $a=b$, on a $a-b=0$. Ainsi :
$(a+c)-(b+c)=a+c-b-c=a-b+c-c=a-b=0$.
Donc $a+c=b+c$.
Propriété : On obtient une nouvelle équation qui a les mêmes solutions que l’équation initiale lorsqu’on multiplie ou on divise par un même nombre non nul les deux membres de cette équation.
Démonstration : Si $a=b$, on a $a-b=0$. Ainsi :
$a\times c-b\times c=(a-b)\times c=0\times c=0$.
Donc $a\times c=b\times c$.
Exemples : Résoudre les équations suivantes :\begin{eqnarray*}
9x&=&-3x+30\\
9x\textcolor{red}{+3x}&=&-3x+30\textcolor{red}{+3x}\\
12x&=&30\\
\dfrac{12x}{\textcolor{red}{12}}&=&\dfrac{30}{\textcolor{red}{12}}\\
x&=&\dfrac{30}{12}
\end{eqnarray*}
La solution de cette équation est $\dfrac{30}{12}$.
On peut noter :
\[S=\{\dfrac{30}{12}\}\]
\begin{eqnarray*}
2,1x-0,4&=&1,3x+0,1\\
2,1x-0,4\textcolor{red}{-1,3x}&=&1,3x+0,1\textcolor{red}{-1,3x}\\
0,8x-0,4&=&0,1\\
0,8x-0,4\textcolor{red}{+0,4}&=&0,1\textcolor{red}{+0,4}\\
0,8x&=&0,5\\
\dfrac{0,8x}{\textcolor{red}{0,8}}&=&\dfrac{0,5}{\textcolor{red}{0,8}}\\
x&=&0,625
\end{eqnarray*}
La solution de cette équation est 0,625.
On peut noter :
\[S=\{0,625\}\]
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |