
Définition : Transformer un point ou une figure par translation c’est faire glisser ce point ou cette figure selon une direction, un sens et une longueur donnés.
Remarque : La translation est symbolisée par une flèche qui donne la direction, le sens et la longueur de ce déplacement.
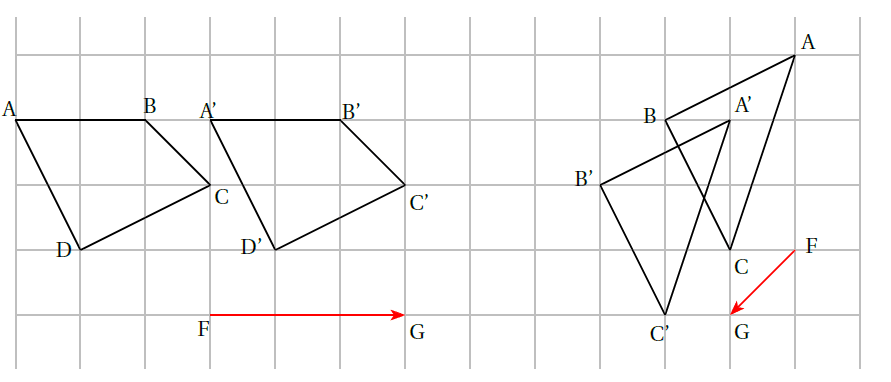
Exemples : Sur les figures ci-dessous, le quadrilatère $A’B’C’D’$ et le triangle $A’B’C’$ sont les images du quadrilatère $ABCD$ et du triangle $ABC$ par la translation qui transforme le point $F$ en $G$. On dit que la translation est de vecteur $\overrightarrow{FG}$.
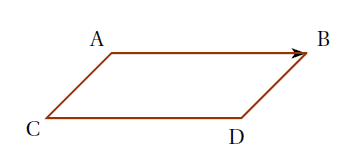
Propriété : Si la translation qui transforme $A$ en $B$ transforme aussi $C$ en $D$, alors $ABDC$ est un parallélogramme éventuellement aplati.
Exemple : Le quadrilatère $ABDC$ est un parallélogramme.
Démonstration : D’après la définition d’une translation, on a :
$AB=CD$ et $(AB)$//$(CD)$.
Un quadrilatère qui possède deux côtés opposés parallèles et de même longueur est un parallélogramme donc $ABDC$ est un parallélogramme.
Propriété : Une translation conserve l’alignement, les longueurs, les angles et les aires.
Exemple : Sur la figure ci-dessous, le triangle $A’B’C’$ est l’image du triangle $ABC$ par la translation qui transforme $E$ en $E’$. On a :
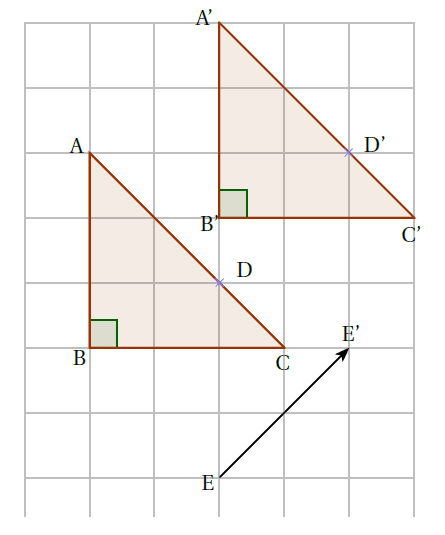 $\text{AB}=\text{A’B’}$
$\text{AB}=\text{A’B’}$Définitions :
Exemples :
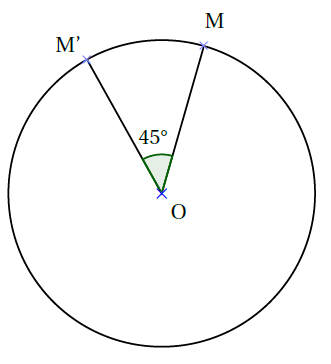
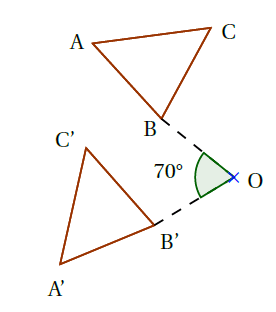
Propriété : Une rotation conserve l’alignement, les longueurs, les angles et les aires.
Exemple : Sur la figure ci-dessous, le triangle $A’B’C’$ est l’image du triangle $ABC$ par la rotation de centre $O$ et d’angle $80$° dans le sens direct.
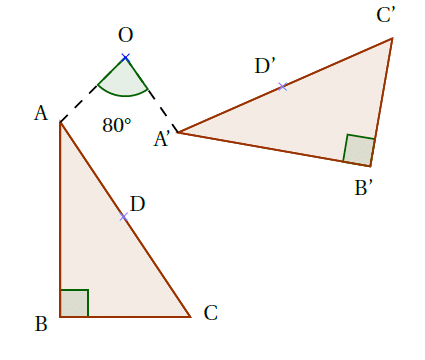 $\text{AB}=\text{A’B’}$
$\text{AB}=\text{A’B’}$| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |