
L’aire d’une figure est la mesure de sa surface intérieure. Donner une unité d’aire permet de mesurer l’aire d’une figure dans cette unité. Quand on change d’unité, la mesure de l’aire change.
Exemple : En prenant un carreau comme unité d’aire, on peut dire que l’aire du polygone ci-dessous est égale à 6 unités d’aire.
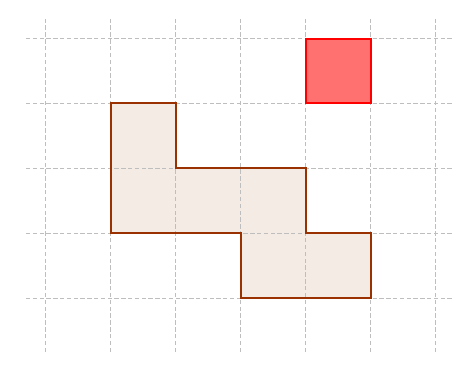
Remarque : Deux figures peuvent avoir le même périmètre mais des aires différentes :
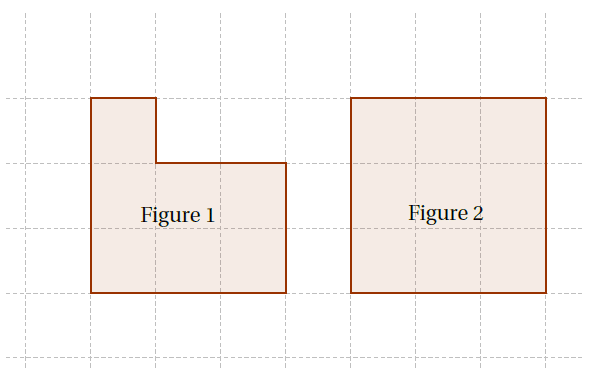
Vocabulaire : Pour les terrains ou les pays on utilise parfois le mot superficie à la place du mot aire.
A chaque unité de longueur (mm, cm, m, dam..) est associée une unité d’aire : $1$ cm$^{2}$ est l’aire d’un carré de côté $1$ cm, $1$ m$^{2}$ est l’aire d’un carré de côté $1$ m…
On remarque que l’on peut placer $100$ carrés de côté $1$ cm dans un carré de côté $1$ dm.
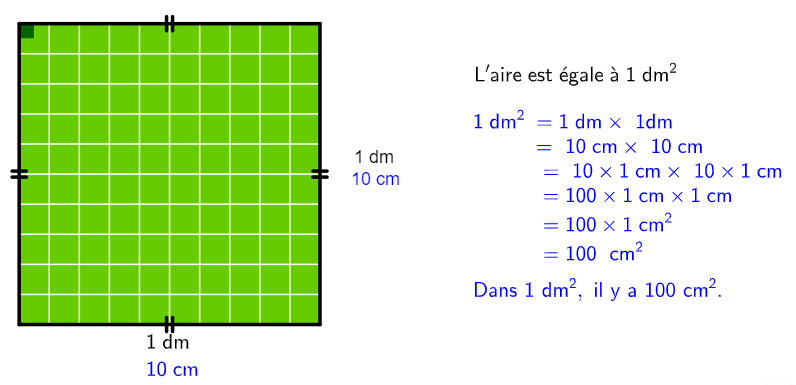
Tableau des unités de surface :

Exemples :
Exemples :
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |