Chapitre 2
Le théorème de Pythagore
Chapitre 2 : Le théorème de Pythagore
A) Racine carré d’un nombre positif
Définition : $a$ désigne un nombre positif. La racine carrée de $a$ est le nombre positif dont le carré est $a$. Ce nombre est notée $\sqrt{a}$ (lire « racine carrée de $a$ ».)
Ainsi,
\[\sqrt{a}>0~~~et~~~\left(\sqrt{a}\right)^{2}=a\]
Exemple : Quelques carrés parfaits à connaître :
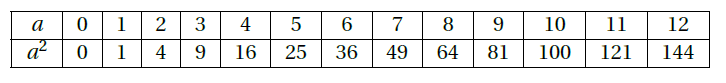
Donc $\sqrt{0}=0$ ; $\sqrt{1}=1$ ; $\sqrt{9}=3$ ; $\sqrt{16}=4$ ; $\sqrt{25}=5$…
Remarque : Il n’existe pas de nombre entier positif dont le carré vaut $27$. Or :
\[5^{2}\leq 27\leq 6^{2}\]Donc $\sqrt{27}$ est comprise entre $5$ et $6$. Pour obtenir une valeur approchée de $\sqrt{27}$, on utilise la calculatrice :
$\sqrt{27}\approx 5,2$.
B) L'égalité de Pythagore
Propriété : Si un triangle est rectangle alors le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés.
Exemple :
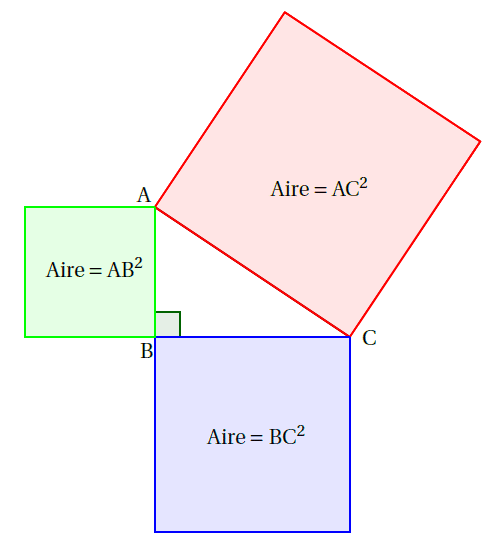
L’égalité de Pythagore : $\text{AC}^{2}=\text{AB}^{2}+\text{BC}^{2}$
Vocabulaire : Dans un triangle rectangle, le côté opposé à l’angle droit s’appelle l’hypoténuse. C’est le plus grand côté du triangle.
Démonstration :
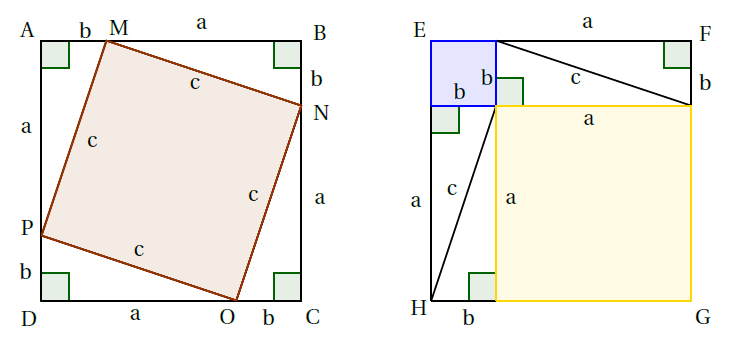
Le quadrilatère $MNOP$ est un losange car il a 4 côtés de même longueur. De plus, la somme des mesures des deux angles aigus d’un triangle rectangle est égale à $90°$. Donc :
$\widehat{\text{DOP}}+\widehat{\text{DPO}}=\widehat{\text{DOP}}+\widehat{\text{CON}}
=90°$.
Ainsi, $\widehat{\text{PON}}=\widehat{\text{DOC}}-90°=180°-90°=90°$.
Le quadrilatère $MNOP$ est un losange possédant un angle droit, c’est donc un carré.
Le quadrilatère $ABCD$ est un carré car il a 4 angles droits et 4 côté de même longueur.
On construit maintenant un quadrilatère $EFGH$ en y replaçant les 4 triangles rectangles.
Le quadrilatère $EFGH$ a 4 côtés de même longueur donc c’est un losange. De plus, il possède un angle droit donc c’est un carré.
Les deux quadrilatères $ABCD$ et $EFGH$ sont deux carrés dont les côtés ont la même longueur, ils ont donc la même aire. Ainsi : $A_{\text{ABCD}}=A_{\text{EFGH}}$.
En observant les deux carrés, on en déduit que l’aire du carré rouge est égale à la somme de l’aire du carré bleu et de l’aire du carré orange. Ainsi :
\begin{eqnarray*}
A_{\text{carré rouge}}&=&A_{\text{carré bleu}}+A_{\text{carré orange}}\\
\text{c}^{2}&=&\text{b}^{2}+\text{a}^{2}
\end{eqnarray*}
Remarque : Ce théorème permet de calculer la longueur d’un des côtés d’un triangle rectangle connaissant les deux autres.
C) Calculer une longueur d’un côté d’un triangle rectangle
Exemple : Le triangle $ABC$ ci-dessous est rectangle en $A$. Calculer la longueur $BC$.
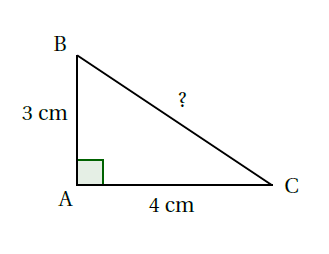
Le triangle $ABC$ est rectangle en $A$.
D’après le théorème de Pythagore :
\begin{eqnarray*}
\text{BC}^{2}&=&\text{AC}^{2}+\text{AB}^{2}\\
\text{BC}^{2}&=&4^{2}+3^{2}\\
\text{BC}^{2}&=&16+9\\
\text{BC}^{2}&=&25\\
\text{BC}&=&\sqrt{25}\\
\text{BC}&=&5~\text{cm}
\end{eqnarray*}
Exemple : Le triangle $DEF$ ci-dessous est rectangle en $E$. Calculer la longueur $EF$.
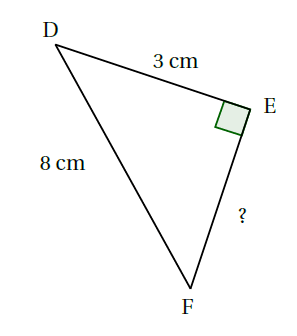
Le triangle $DEF$ est rectangle en $E$.
D’après le théorème de Pythagore :
\begin{eqnarray*}
\text{DF}^{2}&=&\text{ED}^{2}+\text{EF}^{2}\\
8^{2}&=&3^{2}+\text{EF}^{2}\\
64&=&9+\text{EF}^{2}\\
\text{EF}^{2}&=&64-9\\
\text{EF}^{2}&=&55\\
\text{EF}&=&\sqrt{55}\\
\text{EF}&\approx &7,4~\text{cm}
\end{eqnarray*}
Comment je peux trouver l’aire d’un carré mais aven en fonction de à ,b et c ?