Chapitre 21
Egalité de triangles
Chapitre 21 : Egalité de triangles
A) Définition
Définition : Des triangles égaux sont des triangles superposables, c’est à dire qui ont des côtés deux à deux de même longueur et des angles deux à deux de même mesure.
Exemple : Les triangles ci-dessous sont égaux.
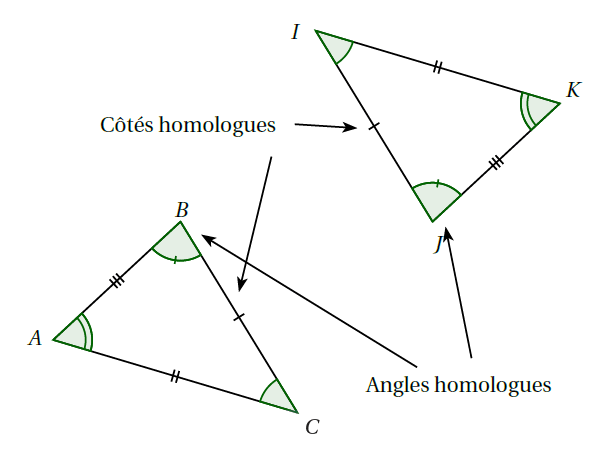
Vocabulaire : Lorsque deux triangles sont égaux, deux angles superposables sont dits angles homologues et deux côtés superposables sont dits côtés homologues.
B) Propriétés
Propriété : Si deux triangles ont un côté de même longueur et des angles adjacents à ce côté deux à deux de même mesure, alors ces deux triangles sont égaux.
Exemple : Les triangles $ABC$ et $TSR$ sont-ils égaux ?
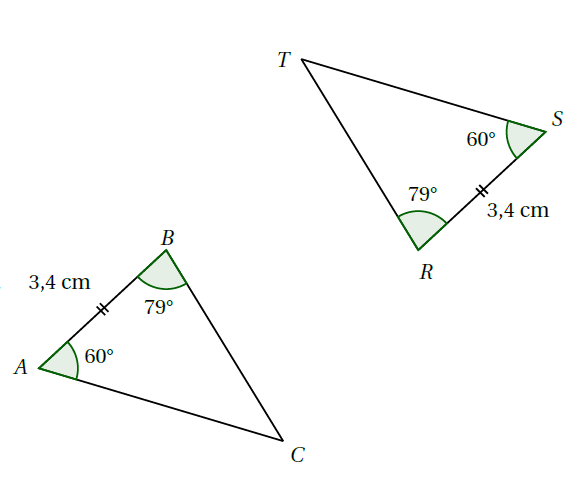
On sait que :
- $AB=RS$
- $\widehat{ABC}=\widehat{TRS}$
- $\widehat{BAC}=\widehat{TSR}$
Ainsi les deux triangles $ABC$ et $TRS$ ont un côté de même longueur et les angles adjacents à ce côté deux à deux de même mesure.
Donc ces deux triangles sont égaux.
Propriété : Si deux triangles ont un angle de même mesure compris entre des côtés deux à deux de même longueur, alors ces deux triangles sont égaux.
Exemple : Sur la figure ci-dessous, les droites $(d_{1})$ et $(d_{2})$ sont parallèles. Montrer que les triangles $EBF$ et $HFC$ sont égaux.
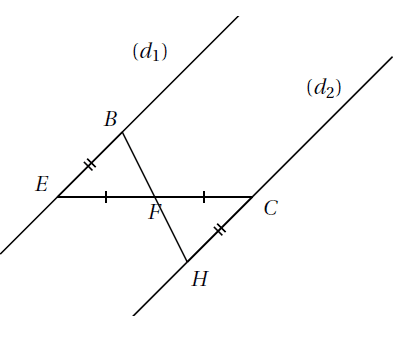
Les droites $(d_{1})$ et $(d_{2})$ étant parallèles, les angles alternes-internes $\widehat{BEF}$ et $\widehat{FCH}$ qu’elles déterminent sont de même mesure. Donc $\widehat{BEF}=\widehat{FCH}$.
De plus, $BE=HC$ et $EF=FC$.
Ainsi les deux triangles $BEF$ et $FHC$ ont un angle de même mesure compris entre deux côtés de même longueur.
Ces deux triangles sont donc égaux.