
Exemple : Une poche de bonbons est partagée entre Maroi et Esteban dans un ratio $3 : 4$ (lire « trois pour quatre»). Cela veut dire que Maroi reçoit $3$ bonbons quand Esteban en reçoit $4$. C’est un partage inégal. Pour une poche contenant $21$ bonbons, représentons les tours de distribution :
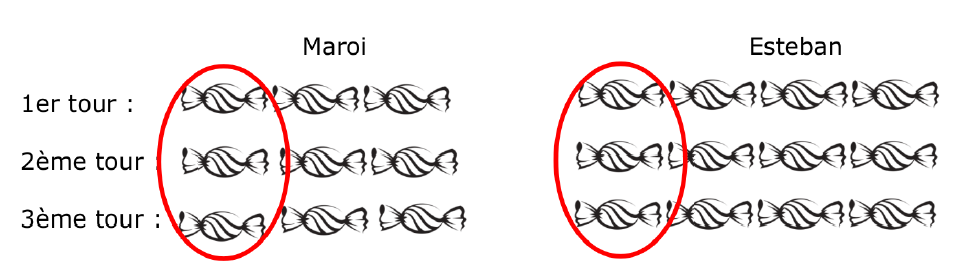
Maroi reçoit donc neuf bonbons quand Esteban en reçoit douze. La quantité de bonbons de Maroi partagée en $3$ est
égale à la quantité de bonbons d’Esteban partagée en $4$.
Définitions :
\[\dfrac{a}{3}=\dfrac{b}{4}\]
\[\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{7}\]

Remarque : un ratio permet de parler des proportions de deux ou trois quantités les unes par rapports aux autres. Notre premier exemple pourrait se traduire aussi par : Maroi a reçu $\dfrac{3}{7}$ des bonbons et Esteban en a reçu $\dfrac{4}{7}$ (le dénominateur a été obtenu en ajoutant le nombre de parts de Maroi et le nombre de parts d’Esteban). Chacune de ces fractions permet de comparer une partie à la
totalité, ce ne sont pas des ratios.
Remarque : En France, on dit que le sexe-ratio est de $105:100$ parce qu’il naît environ $105$ garçons pour $100$ filles.
Exemple : Comment partager $48$ macarons entre Simon et Mandy dans le ratio $5:11$ ?
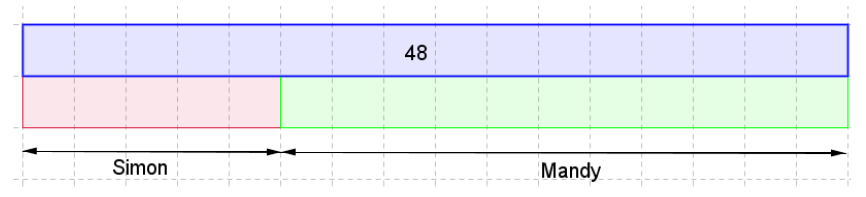
D’après le schéma ci-dessus, $1$ brique unité vaut :
\[48~\text{macarons}\div 16=3~\text{macarons}\]Donc Simon recevra :
\[3~\text{macarons} \times 5=15~\text{macarons}\]Mandy recevra :
\[3~\text{macarons} \times 11=33~\text{macarons}\]
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |