Article écrit par Arham :
I. Introduction
Depuis toujours, la forme de la Terre a suscité de nombreuses questions. Si aujourd’hui on ne peut contredire sa forme sphérique, autrefois, sans les avancés technologiques d’aujourd’hui, la Terre à été représenté de différente formes.
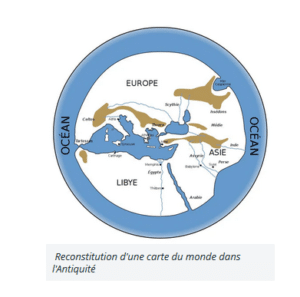
Dès le Ve siècle av. J-C, les philosophes grecs la considère plate. Le monde est représenté en 3 continents: Europe, Asie et Libye. On suggère que le tout est complètement ceinturé par un Océan, s’étendant de l’Europe à la Libye. Cette conception de la Terre fut remise en question dès le IVe siècle av. J-C.
II. Théorie de Platon
Le philosophe grec Platon (v.428-348 av. J-C) propose la forme sphérique de la Terre, en se justifiant par ses deux observations:
– Pendant une éclipse de Lune l’ombre projetée de la Terre est circulaire ;
– La hauteur des étoiles sur l’horizon change lors des déplacements en latitude ; la courbure de la Terre faisant obstacle à une vision complète du ciel, on peut citer l’exemple d’un mat de bateau apparaissant avant la coque.
III. Calculs d’Ératosthène
Platon mourant de phtiriasis, c’est Ératosthène (284-192 av. J-C) qui organise la première estimation précise de la circonférence de la Terre.
Considérant que la Terre est sphérique, part de la constatation suivante :
« A midi, le jour du solstice d’été, dans la ville de Syène (Aujourd’hui Assouan) le soleil éclaire le fond des puits. Le même jour à la même heure à Alexandrie, le soleil n’est pas à la verticale. »
Ératosthène aurait mesuré l’angle entre les rayons solaires et la verticale: 1/50° d’angle plein (un angle plein étant de 360 degrés).
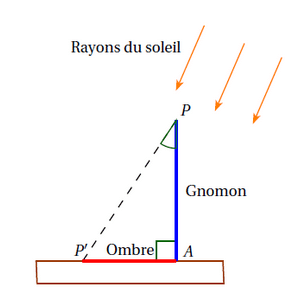
Sur la figure ci-dessus, le point A correspond à Alexandrie, le gnomon est représenté par le segment [AP] et l’ombre du gnomon par le segment [P’A]. Syène et Alexandrie sont approximativement situé sur le même méridien.
Sur la figure ci-dessous, les notations précédentes ont été conservées. Le point S correspond à Syène tandis que le point O au centre de la Terre.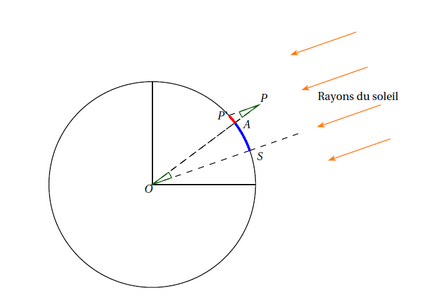
Sachant qu’un angle plein vaut 360°, on en déduit que :
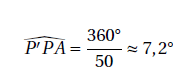
Les rayons du soleil étant considérés comme parallèles car le soleil est très éloigné de la Terre, les deux angles verts (étant alternes-internes) ont nécessairement la même mesure.
On sait que Ératosthène aurait estimé la distance entre Syène et Alexandrie à 5 000 stades Égyptiens (un stade Égyptien mesure ∼ 157,5 mètres). On en déduit que :
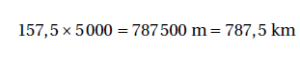
Grace à ces calculs, on peut, à l’aide du tableau de proportionnalité ci-dessous calculer une valeur approchée de la circonférence de la Terre :

Pour faciliter la tache, on utilise l’égalité des produits en croix :
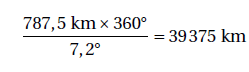
La circonférence de la Terre est donc de 39 375 km. On peut maintenant calculer le rayon de la Terre en utilisant la formule P = 2 x π x R :
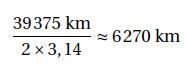
On sait toutefois aujourd’hui que le rayon équatorial de la Terre est d’environ 6378 km. On essaie de calculer le pourcentage d’erreur d’Ératosthène à l’aide du calcul suivant :
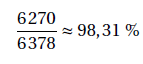
On soustrait ensuite 98.31% à 100 % et on obtient une marge d’erreur de 1.69%. Même avec des erreurs, les calculs d’Ératosthène restent remarquables pour son époque. Ses calculs ont plus tard servis aux navigateurs et aux astronomes.