
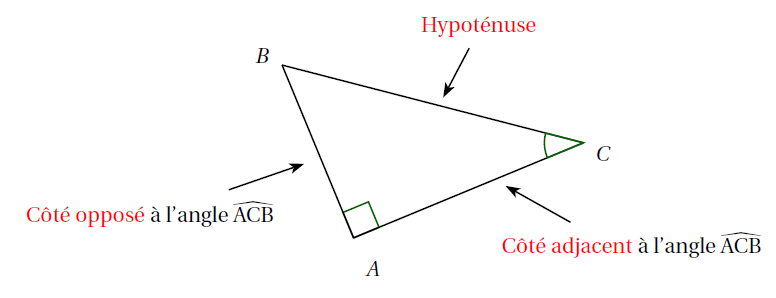
Propriété : Dans un triangle $ABC$ rectangle en $A$, le rapport $\dfrac{BA}{BC}$ ne dépend que de la mesure de l’angle $\widehat{ABC}$.
Démonstration : Sur la figure ci-dessous, $ABC$ est un triangle rectangle en $A$ et $A’BC’$ est un triangle rectangle en $A’$. Ces deux triangles ont leur angle aigu de sommet $B$ en commun.
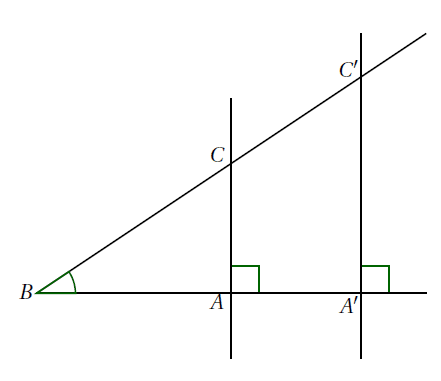
Les droites $(AC)$ et $(A’C’)$ sont toutes les deux perpendiculaires à la droite $(AB)$ donc elles sont parallèles entre elles.
$A$ appartient au côté $[BA’]$.
$C$ appartient au côté $[BC’]$.
D’après le théorème de Thalès :
\[\dfrac{BA}{BA’}=\dfrac{BC}{BC’}(=\dfrac{AC}{A’C’})\]L’égalité des produits en croix permet d’écrire :
\[BA\times BC’=BC\times BA’\]Ainsi :
\[\dfrac{BA\times BC’}{BC\times BC’}=\dfrac{BC\times BA’}{BC\times BC’}\]Donc :
\[\dfrac{BA}{BC}=\dfrac{BA’}{BC’}\]Donc, le rapport $\dfrac{BA}{BC}$ dépend uniquement de la mesure de l’angle $\widehat{ABC}$.
Définition : Dans un triangle rectangle, le cosinus d’un angle aigu est égal au rapport:
\[\dfrac{\text{longueur du côté adjacent à cet angle}}{\text{longueur de l’ hypoténuse}}\]
Exemple :
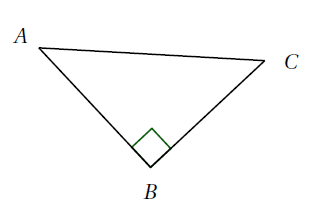
\[cos(\widehat{BAC})=\dfrac{AB}{AC}\]\[cos(\widehat{ACB})=\dfrac{BC}{AC}\]
Remarques :
Exemple : Soit $ABC$ un triangle rectangle en $C$ tel que $AB=5~\text{cm}$ et $\widehat{ABC}=25$°. Calculer la longueur $BC$, arrondir au dixième.
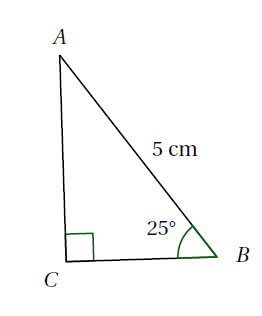
Le triangle $ABC$ est rectangle en $C$:
\begin{eqnarray*}
cos(\widehat{ABC})&=&\dfrac{BC}{AB}\\
cos(25\text{°})&=&\dfrac{BC}{5}\\
\dfrac{cos(25\text{°})}{1}&=&\dfrac{BC}{5}\\
BC&=&\dfrac{5\times cos(25\text{°})}{1}\\
BC&\approx &4,5~~\text{cm (On utilise la touche cos de la calculatrice).}
\end{eqnarray*}
Exemple : Soit $ABC$ un triangle rectangle en $C$ tel que $AC=2~\text{cm}$ et $BC=5~\text{cm}$. Calculer la mesure de l’angle $\widehat{BAC}$, arrondir au degré près.
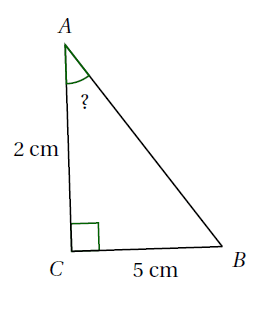
Le triangle $ABC$ est rectangle en $C$, d’après le théorème de Pythagore :
\begin{eqnarray*}
AB^{2}&=&AC^{2}+BC^{2}\\
AB^{2}&=&2^{2}+5^{2}\\
AB^{2}&=&4+25\\
AB^{2}&=&29\\
AB&=&\sqrt{29}\\
AB&\approx &5,4~\text{cm}
\end{eqnarray*}
\begin{eqnarray*}
cos(\widehat{BAC})&=&\dfrac{AC}{AB}\\
cos(\widehat{BAC})&=&\dfrac{2}{5,4}\\
\widehat{BAC}&\approx &68\text{° (On utilise la touche arccos de la calculatrice).}
\end{eqnarray*}
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |