
Lors d’un trajet en voiture, la vitesse n’est pas constante (accélérations, ralentissements…). La vitesse moyenne est la vitesse qu’aurait cette voiture si elle parcourait la même distance dans le même temps en conservant toujours la même vitesse.
Propriété : Dire que $v$ est la vitesse moyenne lors d’un trajet signifie que la distance parcourue $d$ est proportionnelle à la durée $t$ du trajet.
Le coefficient de proportionnalité est la vitesse moyenne $v$.
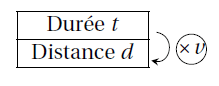
Ainsi :
\[d=v\times t\]
Conséquence : La vitesse moyenne sur un trajet est le quotient de la distance parcourue $d$ par la durée $t$ du trajet.
\[v=\dfrac{d}{t}~~~~\text{et}~~~~t=\dfrac{d}{v}\]
Exemple : Calcul d’une vitesse moyenne
Un automobiliste a parcouru $98~\text{km}$ en $1~\text{h}10~\text{min}$. Calculer sa vitesse moyenne en km/h.
$1~\text{h}10~\text{min}= 70~\text{min}$
\begin{eqnarray*}
v&=&\dfrac{d}{t}\\
v&=&\dfrac{98~\text{km}}{70~\text{min}}\\
v&=&1,4~\text{km/min}\\
v&=&1,4\times 60~\text{km/h}\\
v&=&84~\text{km/h}
\end{eqnarray*}
Cet automobiliste a roulé à une vitesse moyenne de $84~\text{km/h}$.
Exemple : Calcul d’une distance
Un randonneur a marché à une vitesse de $5,6~\text{km/h}$ pendant $2~\text{h}30~\text{min}$. Quelle distance a-t-il parcourue ?
$2~\text{h}30~\text{min}=2,5~\text{h}$
\begin{eqnarray*}
d&=&v\times t\\
d&=&5,6~\text{km/h}\times 2,5~\text{h}\\
d&=&14~\text{km}
\end{eqnarray*}
Ce randonneur a parcouru $14~\text{km}$ en $2~\text{h}30~\text{min}$.
Exemple : Calcul d’une durée
Un skieur parcourt une descente de ski de $1~\text{km}$ à la vitesse de $252~\text{km/h}$. Quelle est la durée de la descente ?
\begin{eqnarray*}
t&=&\dfrac{d}{v}\\
t&=&\dfrac{1~\text{km}}{252~\text{km/h}}\\
t&\approx &0,004~\text{h}\\
t&\approx &0,004\times 3~600~\text{s}\\
t&\approx &14,4~\text{s}
\end{eqnarray*}
La durée de cette descente est d’environ $14,4~\text{s}$.
| Cookie | Durée | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |