Chapitre 9

Angles et parallélisme

cours de 5ème

Chapitre 9 : Angles et parallélisme

A) Vocabulaire

Définition : Deux angles opposés par le sommet ont le même sommet et des côtés dans le prolongement l’un de
l’autre.

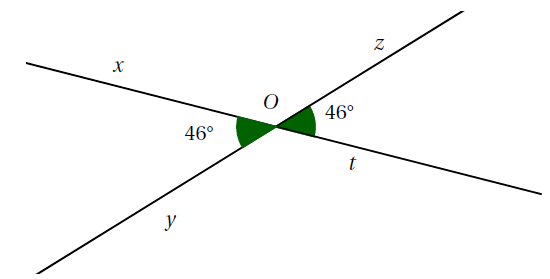
Exemple : Sur la figure ci-dessous, les angles xOy^ et zOt^ sont opposés par le sommet. Ils ont donc la même mesure.

Deux angles opposés par le sommet

Exemple : Sur la figure ci-dessous, les droites (d) et (d′) sont coupées par la sécante (Δ).

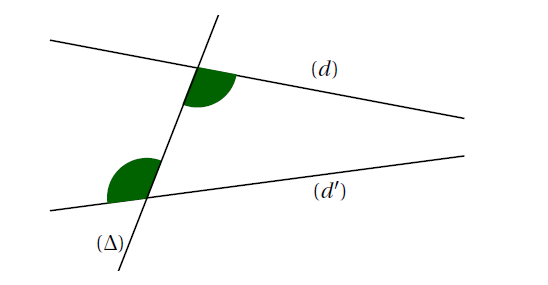
Deux angles alternes-internes
Les angles codés en vert sont des angles alternes-internes.

Exemple : Sur la figure ci-dessous, les droites (d) et (d′) sont coupées par la sécante (Δ).

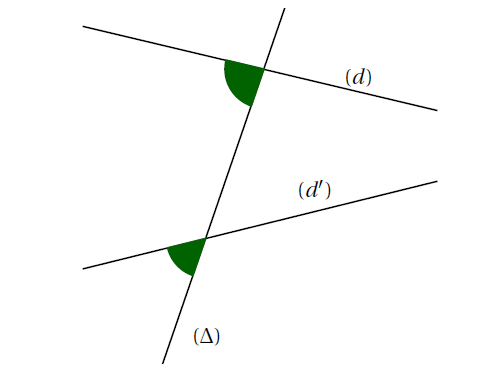
Deux angles correspondants
Les angles codés en vert sont des angles correspondants.

B) Propriétés

Propriété : Si deux droites parallèles sont coupées par une sécante, alors les angles alternes-internes (ou correspondants) qu’elles forment ont la même mesure.

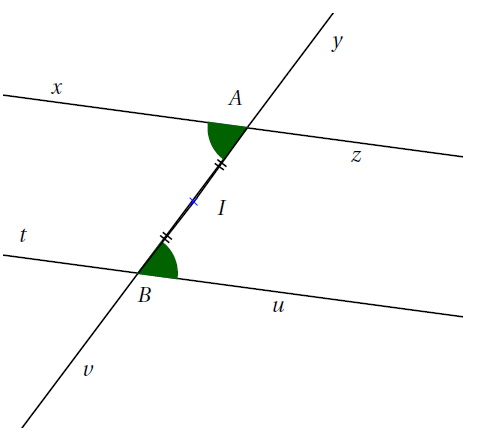
Démonstration : Les angles xAv^ et yBu^ sont alternes-internes.
Soit I le milieu du segment [AB]. Le symétrique de l’angle xAv^ par rapport au point I est l’angle yBu^.
Or la symétrie centrale conserve la mesure des angles.
Donc xAv^=yBu^.

Pourquoi deux angles alternes-internes ont la même mesure ?

Exemple : Sur la figure ci-dessous, la droite (CH) coupe les droites parallèles (BD) et (FG) respectivement en A et E.

Calculer la mesure de l’angle FEA^.

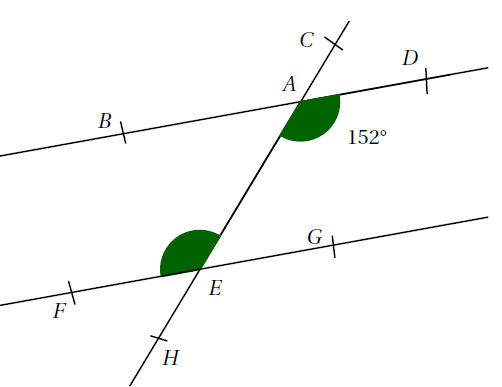
Deux angles alternes-internes de même mesure
Les angles FEA^ et EAD^ sont alternes-internes. Comme les droites (BD) et (FG) sont parallèles alors ces deux angles ont la même mesure. Donc:
FEA^=EAD^=152°

Propriété : Si deux droites coupées par une sécante forment deux angles alternes-internes (ou correspondants) de même mesure, alors ces droites sont parallèles.

Exemple : Sur la figure ci-dessous, la droite (PK) coupe la droite (IL) en J et la droite (MO) en N.

Prouver que les droites (IL) et (MO) sont parallèles.

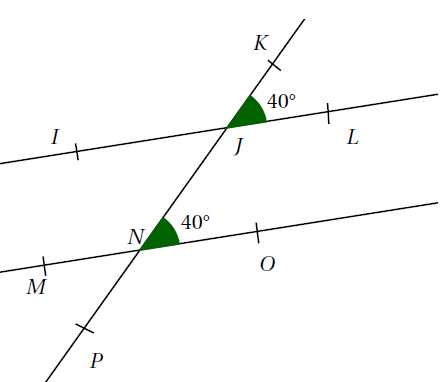
Une démonstration du parallélisme de deux droites
Les angles KJL^ et JNO^ sont correspondants. Or, ils ont la même mesure. Donc les droites (IL) et (MO) sont parallèles.

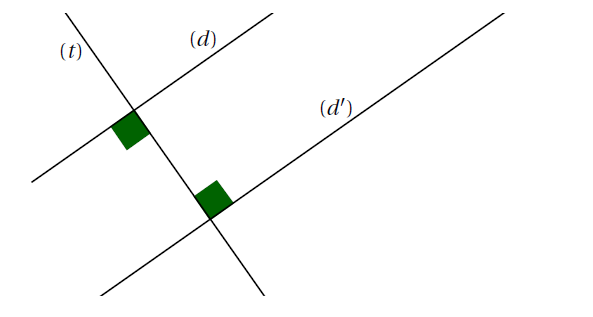
Remarque : Si deux droites (d) et (d′) sont perpendiculaires à une même droite (t), alors (d) et (d′) sont parallèles. On retrouve le cas étudié en 6ème…

Deux droites perpendiculaires à une même droite sont parallèles

Exercices corrigés
J'accède à d'autres documents

Vous pourriez aimer:

  1. Chapitre 19 : Somme des mesures des angles d’un triangle
  2. Chapitre 6 : Addition, soustraction et multiplication
  3. Chapitre 3 : Droites sécantes, parallèles et perpendiculaires

Laisser un commentaire